- #1
mathlearn
- 331
- 0
Here is the Problem
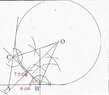
View attachment 6180
Here is the construction, Hoping that I have done it correct "State with reasons that $\angle$ ACB is bisected by line OC"
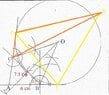
View attachment 6181
Many THanks (Party)
View attachment 6180
Here is the construction, Hoping that I have done it correct "State with reasons that $\angle$ ACB is bisected by line OC"
View attachment 6181
Many THanks (Party)
Attachments
Last edited: