Static equilibrium helpprobably simple

[Juntao]

I've added a picture.

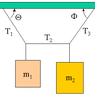
The system shown to the right is in equilibrium with the center string exactly horizontal.
Mass # 1 = 42 kg.
Mass # 2 = 50 kg.
È = 31 degrees.
===========
A) Tension in left most string?
B) Tension in center string?
C) Tension in right string?
D) What is the angle Ö on the right string?

=======
a) Not too bad at all. Just did sin 31=(m1*g)/T1
T1=799.16N

b) Now I'm stuck. It probably is really easy, but I'm missing something. I drew the FBD, and so I got a force from m1 and m2 downwards, a T1 force to the left, and a T3 force to the right. But its not helping much, at least to me. Yes, its a static equilibrium equation, so sum of all forces in x and y and torques equal zero, but I don't know where to start correctly.

 

[Doc Al]

Originally posted by Juntao
b) ... Yes, its a static equilibrium equation, so sum of all forces in x and y and torques equal zero, but I don't know where to start correctly.

Start by considering the forces acting at the "knots" (the places where the strings tie together). For the left knot, setting vertical forces equal to zero is what gave you your first answer. So keep going! Set the horizontal forces to zero. Then do the same for the right knot.

 

[jamesrc]

Look at the node on the left side where the 3 strings meet. Summing the forces in the x-direction gives

T_1\cos\Theta = T_2

For the node on the right side,

T_2 = T_3\cos\Phi

(And your other equation is T_3\sin\Phi = m_2g. Combined with the other equation you have, that's 4 equations and 4 unknowns.)

 

[exequor]

hey you have to solve for one force then that would help you find the others. i am sort of busy but i will try my best.

t1 sin angle1 = m1 * g
t3 sin angle2 = m2 * g
t1 cos angle1 = t3 cos angle2 and this would be equal to the tension in t2.