BurpHa
- 47
- 14
- Homework Statement
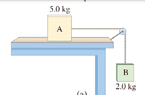
- For the system of Fig. 4–32 (see below), how large
a mass would box A have to have to prevent any motion
from occurring? Assume the coefficient of the static friction = 0.30.
- Relevant Equations
- Newton's Third Law, Newton's Second Law.
Ok, logically, it must be that the static friction force of block A equal to the force of gravity on block B, so mass of block A is:
m_A * 9.8 * 0.30 = m_B * 9.8
m_A * 2.94 = 2 * 9.8
m_A * 2.94 = 19.6
m_A \approx 6.7 kg.
However, when I look at block A individually, there is one thing confuses me.
Say block A's mass is x, then in the frictionless scenario, tension force on block A is:
\frac 19.6 {x + 2} * x
I wonder how about if the static friction of block A is equal to the tension force on block A, because then block A should be stopped. Then:
9.8 * x * 0.3 = \frac 19.6 {x + 2} * x
9.8 * 0.3 = \frac 19.6 {x + 2}
2.94 = \frac 19.6 {x + 2}
x \approx 4.7 kg.
According to Newton's second law, then block A cannot move, because the force of tension and the force of static friction cancel out, thus, block B cannot move. So what is wrong about this thinking?
This is why it is confusing. I can understand how all of this work at the bird's eye view, but when I get to the individual level, it starts to confuse. I know my question is kind of silly, but please clarify for me.
Thank you for your help.
m_A * 9.8 * 0.30 = m_B * 9.8
m_A * 2.94 = 2 * 9.8
m_A * 2.94 = 19.6
m_A \approx 6.7 kg.
However, when I look at block A individually, there is one thing confuses me.
Say block A's mass is x, then in the frictionless scenario, tension force on block A is:
\frac 19.6 {x + 2} * x
I wonder how about if the static friction of block A is equal to the tension force on block A, because then block A should be stopped. Then:
9.8 * x * 0.3 = \frac 19.6 {x + 2} * x
9.8 * 0.3 = \frac 19.6 {x + 2}
2.94 = \frac 19.6 {x + 2}
x \approx 4.7 kg.
According to Newton's second law, then block A cannot move, because the force of tension and the force of static friction cancel out, thus, block B cannot move. So what is wrong about this thinking?
This is why it is confusing. I can understand how all of this work at the bird's eye view, but when I get to the individual level, it starts to confuse. I know my question is kind of silly, but please clarify for me.
Thank you for your help.