Statics. Equilibrium With Springs and Tension Question.

[Dieinhell100]

Homework Statement

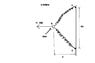
The springs BA and BC each have a stiffness of 500N/m and an unstretched length of 3m. Determine the displacement d of the cord from the wall when a force F = 175N is applied to the cord.

Homework Equations

F=ks
ƩFx=0
ƩFy=0

The Attempt at a Solution

This is as far as I got. I set out the sum of the forces in the x and y direction, assuming left is positive x and up is positive y. I don't know what to do from here with the information they have given me.

ƩFx=F-Tᴮᴬcosθ -Tᴮᶜcos(θ)=0
ƩFy=Tᴮᴬsinθ-Tᴮᶜsinθ=0
Tᴮᴬ=ks=500N/m * (l-3m)
Tᴮᶜ=ks=500N/m * (l-3m)

I'm not sure what to do when I don't have the angles or the stretched length. Attached is a drawing I made of the problem (excuse me for my messiness).

 

[voko]

The angles and the stretched length are related to the other side of the triangle.

 

[Dieinhell100]

The angles and the stretched length are related to the other side of the triangle.

I don't understand..?

What other side of the triangle?

And if it helps, the solution the book gives me is d=1.52m

 

[voko]

You can assume that the force of tension and the stretched lengths are equal in both springs due to symmetry. The two springs and the wall thus form an isosceles triangle. So you can relate the angle of inclination with the stretched length of the springs. That gives you another equation. You end up having three equations with three unknowns (force of tension, angle, length of the springs).

 

[azizlwl]

Very interesting problem.
Since we have the solution, i think you should work backward to check on the given data or we need different approach such as conservation of energy or conservative force.

 

[bigu01]

175=2Tsin(theta)

87.5=Tsin(theta)

87.5=T[d^2/(√(3^2+d^2))]

T=ks=500*(√(3^2+d^2)-3)

d*(1-3/(√(9+d^2))=0.175

d=1.56

 

[haruspex]

175=2Tsin(theta)

87.5=Tsin(theta)

87.5=T[d^2/(√(3^2+d^2))]

T=ks=500*(√(3^2+d^2)-3)

d*(1-3/(√(9+d^2))=0.175

d=1.56

The protocol on this forum is to nudge in the right direction, not post complete solutions.
And you have a typo in the third line.

 

[bigu01]

The protocol on this forum is to nudge in the right direction, not post complete solutions.
And you have a typo in the third line.

Sorry,as you could see that was my first post, and I was trying to solve that question very hard.After doing it, I was so happy that I decided to share it with the others.Next times will not do that.

 

[nasu]

Never mind.

 

[shaggy22]

I have this same problem and can't figure it out for the life of me. I have been working the problem for a good 2 hours now. I got
175=2Tsin(theta)
175=2T[d/(sqrt(9+d^2))]
then I replaced T with kd since T=kd
so
87.5=500[d^2/(sqrt(9+d^2)]

Can someone tell me if this is correct so far because when i simplify for d I can't seem to get the right answer.