Engineering Statics of Rigid Bodies - Why is the normal force not considered?

[Nova_Chr0n0]

Homework Statement

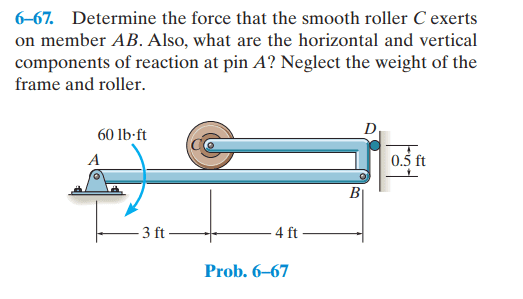
6–67. Determine the force that the smooth roller C exerts
on member AB. Also, what are the horizontal and vertical
components of reaction at pin A? Neglect the weight of the
frame and roller.

Relevant Equations

Equilibrium Equations

The problem is from Hibeller's book, Mechanics: Statics and attached below is the picture of the problem:

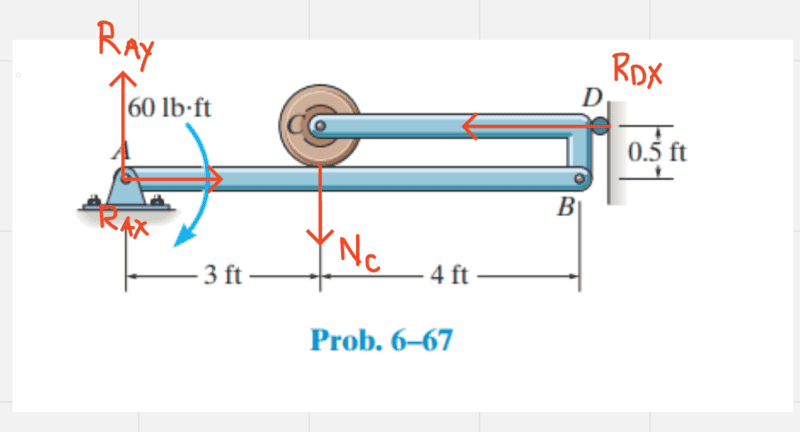
My question about this problem is about the FBD of the reactions. Here is how I drew it:

But when I tried checking the solution for the problem, they have this as their FBD:

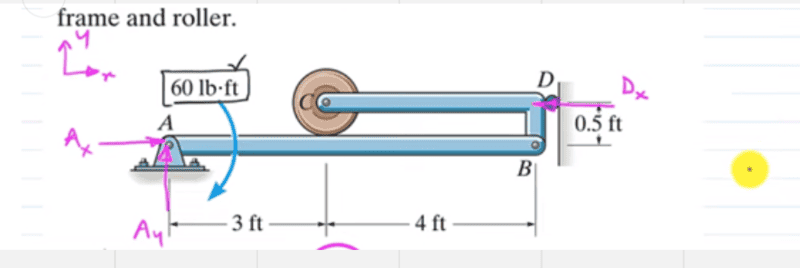
My question is, why did they not include the Normal force created by the roller? Is it not considered as a reaction for the whole figure? I think I'm missing an important concept here and it confuses me. This topic is Frames and Machines.

 

[BvU]

Hi,

A free free body diagram considers forces that are external to the body

$\$

 

[Lnewqban]

Please, see:
https://en.m.wikipedia.org/wiki/Overdetermined_system

Resolving external forces with three available equations (summation of external forces and moments) is the first step.
With those values, you can calculate the internal forces and moments in any armature, frame, truss or mechanism.

For practical purpose, you could weld that roller to member AB, and both members at pin B, without modifying the shown conditions.
Its normal force can be considered an internal force of the whole mechanism.

Note that a Dy reactive force is needed to keep the static equilibrium.
You could simplify the "body" to a single member being wedged against the vertical surface by the applied clockwise moment (like shown below).
Dy is preventing the body from rotating about pivot A.

Dx will induce a moment on member BDC about pin B, which will translate into the roller normal force that you have mentioned (which will be a bending load on member AB).

As you can see, we need to calculate the chain reaction step by step, beginning with reaction forces at B and D.

 

[Nova_Chr0n0]

Sorry, I am really slow to catch up, so I need more clarification. My current understanding, based on the explanation, is that:

The normal force produced by the roller is considered an internal force and not an external force. Is it because the roller is part of the whole figure and therefore its normal force is not considered an external one? Here is what I'm thinking right now: Consider a box and a surface:

Here, the box is the figure and is experiencing a normal force. This normal force is exerted by the surface (which is a different figure that is not being examined) and not the box, so is it considered an external force?

In the figure I've shown, the red colors are an external object to the figure (highlighted as yellow) and are therefore considered an external force?

 

[BvU]

This normal force is exerted by the surface (which is a different figure that is not being examined) and not the box, so is it considered an external force?

Yes

In the figure I've shown, the red colors are an external object to the figure (highlighted as yellow) and are therefore considered an external force?

Yes