mhrob24
- 53
- 9
- Homework Statement
- Draw the FBD of the Backhoe as shown in the figures
- Relevant Equations
- M=0
Fx=0
Fy=0
So, for the link "AB"...they didn't directly list the pin reactions from pin "A" here, but I want to be sure that I understand what those reactions are. So, from what I see in this image, the member is pushing at the pin "A" (red arrow) because otherwise, the bucket would want to rotate counterclockwise (blue arrow). That means that the pin "A" reaction on the member "AB" is also pushing back against member "AB" (green arrow), so it's a two-force member with compression forces at each end. I THINK the book is showing the same thing, because if you look at what they have for the FBD of pin "B", they have the member "AB" at "B" pushing against pin "B", so the reaction from pin "B" will push back against it; just like pin "A" does.
Is this correct? I have another question about how this book drew the forces, but I’ll ask after I clarify this…
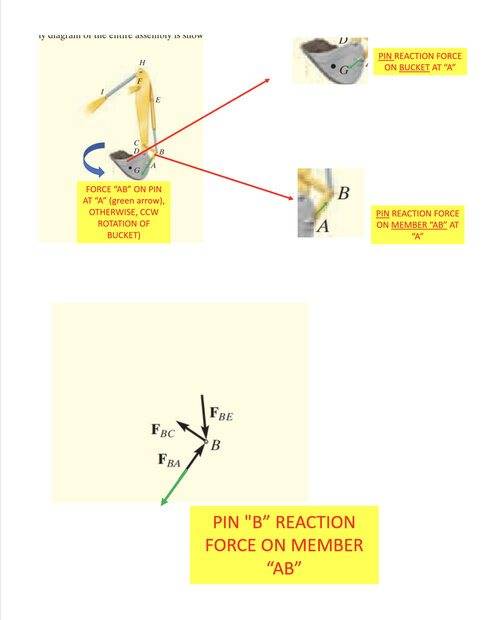
Is this correct? I have another question about how this book drew the forces, but I’ll ask after I clarify this…