Statics: When the reactions depend on the displacements

[Juanda]

TL;DR Summary

When the reactions depend on the displacements the problem cannot be solved with the typical tools from statics. What tools should I use?

In some problems, there is a dependency between the reactions at the supports and the displacements due to the deformations. In such cases, typical tools from statics and resistance of materials cannot be used. I believe that is because one of the main assumptions is that only very small deformations will happen.
What is the name for problems where this dependency exists? Do you recommend a particular book about them?

Let's start with a simple example.

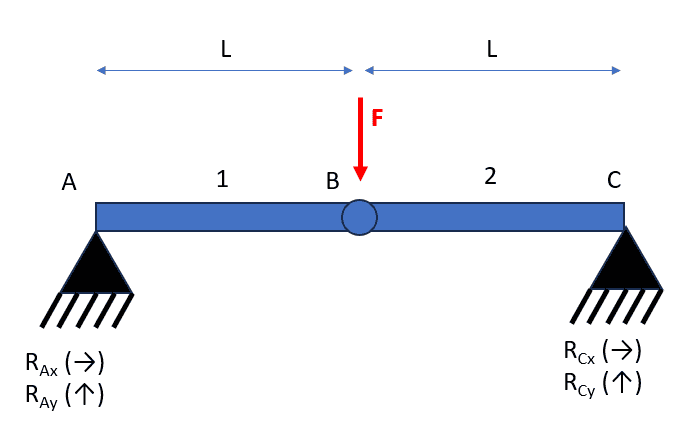
This problem is statically undetermined because the 3 equations of equilibrium are not enough to find the reactions but that's not the point. The point is that those rods can only work axially because it's a truss with forces only in the articulations so to counteract ${\color{Red} F}$ that has a vertical component (and only a vertical component in this simple example) they will need to change their orientation so that the axial internal forces have a vertical component too.

The problem can be solved by finding the relation between the internal axial forces in the beam and the deformation of the system.

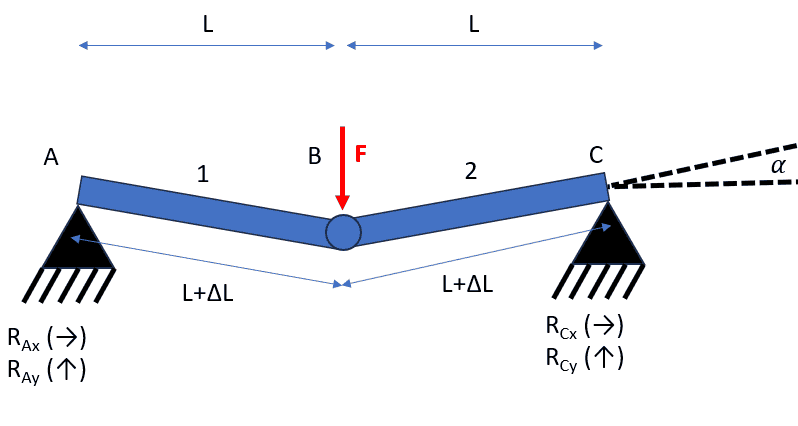
Now using the equilibrium of vertical forces at the joint B it is possible to find the reactions, internal forces, elongation, and the angle the system will adopt.
$\sum F_y=0 \rightarrow -F+N_{1_y}+N_{2_y}=0 \left \{ Symmetry \rightarrow N_{1_y}=N_{2_y}=N_y;N_y=Nsin(\alpha);N=k\Delta L\right \} \rightarrow$
$\rightarrow F=2k\Delta L\sin\alpha$
That's still not enough because in that equation we don't know 2 variables $(\Delta L, \alpha)$. However, it is possible to link them.

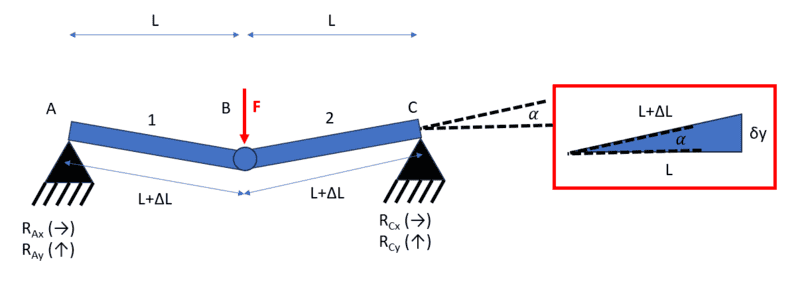
$(L+\Delta L)\cos\alpha = L\rightarrow \Delta L = \frac{L}{\cos\alpha}-L$

Then, by combining the two previous equations, it is possible to have only 1 variable to solve.
$F=2k\Delta L\sin\alpha\rightarrow F=2k(\frac{L}{\cos\alpha}-L)\sin\alpha\rightarrow \frac{F}{2KL}=\tan\alpha-\sin\alpha$
I'm pretty sure that trigonometric equation cannot be solved analytically so I will leave it there. The point is that it can be solved and the system is fully defined. As a sanity check, as $\alpha \rightarrow 0$ it seems like the equation fails. However, if $\alpha \rightarrow 0$ is because then $k\rightarrow \infty$ so we have a $\infty \times 0$ situation which can spit $F$ as a result.

So the problem is solvable. However, the procedure is very different when comparing it with the linear problems we typically see in books on Static and Resistance of Materials. Even for this simple case, I'm not certain I could solve it if I got rid of all the symmetries. Is there an established way to solve these types of problems/structures?

Another case that could be interesting to solve is the following

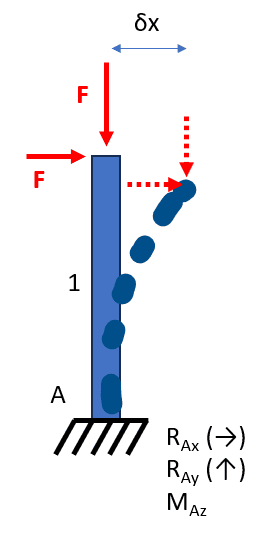
I don't know if that's related to how the formulas for buckling are derived but I doubt it because when checking for buckling, at no point the reaction moment $M_{A_z}$ is considered. Is this maybe an alternative way of checking for buckling? The point is that as $\delta x$ increases, the reaction $M_{A_z}$ needs to grow as well to compensate $F \delta x$ so we have a problem where again the reactions depend on the displacements. I tried solving this problem with no luck so far.
Do you know the standard procedure to solve it? Or books that cover this?

 

[T1m0]

This is a case of a beam under combined axial and transverse loading (Beam-columns). The displacement formula for your specific case can be found in Roark's Formulas for Stress and Strain. Techniques for analyzing these types of problems can be found in textbooks on Advanced Mechanics of Materials (e.g., Cook ang Young's book)

 

[Juanda]

This is a case of a beam under combined axial and transverse loading (Beam-columns). The displacement formula for your specific case can be found in Roark's Formulas for Stress and Strain. Techniques for analyzing these types of problems can be found in textbooks on Advanced Mechanics of Materials (e.g., Cook ang Young's book)

I just read Chapter 12 in Roark's and at no point, it mentions the displacements and how the reactions depend on it.

I'm sure the information in there is of big importance but it's not what I'm looking for.

In Chapter 15 I could find some information more directly related to the original post.

After reading the chapter I still do not know how to solve the problem but at least now I know the name of the area that covers this kind of thing.
I'll keep reading about it. Maybe, in the meantime, someone can provide some insight about what I posted or specific references to study.

 

[T1m0]

In Roark's book, there should be a section on "Beams Under Simultaneous Axial and Transverse Loading." If P is the axial load and W is the transverse load at the end, then the transverse end deflection is

y=W/(k*P)*(tan(kL)-kL) where k=(P/(EI))^(1/2) and L is the length of the beam.

 

[Juanda]

I just checked section 8.7 BEAMS UNDER SIMULTANEOUS AXIAL AND TRANSVERSE LOADING and I couldn't find the formula you mention.
Are we maybe seeing different editions?
Anyways, I find Roark's book very difficult to understand. All the formulas are cramped in there without much background or explanatory pictures. It's a book for formulas after all so I understand it's got a specific purpose. It's just not aligned with what I'm looking for.
I'll try to find a book about Elastic Stability to give it a shot and try to understand the math behind the concept. Timoshenko seems to have a book about it but it's too hard for me to understand. I'll have to try a different source where the explanations are more chewed for the reader.

 

[T1m0]

I agree that Roark's book is not very useful for learning analysis techniques. If you want to ease into the subject, I suggest that you start with a basic book on Mechanics of Materials. Typically, there will be a chapter on bucking of beams where there will be a section on columns with eccentric axial loads. This will not correspond directly to your case, but the analysis technique used there is similar to what you will need to address the problem that you posed.

 

[Juanda]

I think I have some new insight into this problem.

The problem would be solvable in time if the elements were capable of dissipating energy. It'd be done by a computer with FEA but I don't have access to that and I also think it'd be computationally expensive so I'll ignore that approach. I did something similar once to calculate catenaries in Python and it's not nice.

For quite a while, I have been thinking about solving it iteratively, but I don't think that converges because the leverage will be greater in each iteration.
Today I was reading the wiki page for Euler's buckling and I gave it a shot although I cannot solve it entirely. By the way, after seeing the derivation for Euler's buckling, I realized it looked similar to what I posted originally. The point is to assume the deformation and write equilibrium in the deformed state.

Making equilibrium in the deformed state around A:
$$M_A - F_yx_{B'} - F_x y_{B'}=0 $$

For that, I'd need the coordinates of $B'$ for which I'd need to know the deformation beforehand. It's kind of a vicious circle. The way I think to break it is by using the bending diagram and assuming the simplifications given by the Bernoulli-Euler beam formulation, it's possible to find the new $y_{B'}$.
Note: Those simplifications imply $x_B=x_{B'}=l$. That is impossible but the point is to simplify the problem by only calculating the factors with the greatest impact.



$$M(x)=-EI\frac{d^2y}{dx^2}$$

From the bending diagram, $M(x)$ can be obtained.
$$M(x)=C_1x+C_2$$
$$M(x=l)=0$$
$$M(x=0)=F_y l + F_x y_{B'}$$
Solving the system of equations.
$$M(x)=-\frac{F_y l+F_x y_{B'}}{l}x+F_y l+F_x y_{B'}$$

Finally, combining that with the previous expression relating bending and deformation:
$$-\frac{F_y l+F_x y_{B'}}{l}x+F_y l+F_x y_{B'}=-EI\frac{d^2y}{dx^2}$$

And that's where I don't know how to continue because $y_{B'}$ is not just $y$. If that were the case, it'd be a differential equation that I wouldn't know how to solve either right now but I'd be more familiar with it. The problem is that $y_{B'}$ is the value taken by $y$ at $B$. Mathematically expressed it'd be $y(x=l)=y_{B'}$.

Do you think this approach to the problem makes sense?
If so, do you know how to tackle such a differential equation?

 

[Juanda]

If so, do you know how to tackle such a differential equation?

The value of $y_{B'}$ is unknown but it must be just a number because it's evaluated $y(x=l)=y_{B'}$ so I could treat it as a constant. It means I can solve the differential equation as usual.
Then, using boundary conditions, I know the displacement and slope at $y(x=0)$ which will give me two equations. But I'm still missing one equation to be able to find the last unknown $y_{B'}$.

 

[T1m0]

In your cantilever beam example, you did not get the internal bending moment quite right because you assumed that it was simply a linear function of x. I suggest that you get the moment by cutting the beam at some position x and drawing a free body diagram. This will lead to the following expression for moment

M(x)=-F_x*(y_B-y(x))-F_y*(L-x)

This will give you a differential equation for y(x). Then solve the differential equation using the boundary conditions

At x=0, y=0
At x=0, dy/dx=0
At x=L, y=y_B

This is not too difficult, but the algebra gets messy.

 

[erobz]

In your cantilever beam example, you did not get the internal bending moment quite right because you assumed that it was simply a linear function of x. I suggest that you get the moment by cutting the beam at some position x and drawing a free body diagram. This will lead to the following expression for moment

M(x)=-F_x*(y_B-y(x))-F_y*(L-x)

This will give you a differential equation for y(x). Then solve the differential equation using the boundary conditions

At x=0, y=0
At x=0, dy/dx=0
At x=L, y=y_B

This is not too difficult, but the algebra gets messy.

Does $\frac{d^2y}{dx^2} = \frac{M(x)}{EI}$ even hold? What @Juanda seems to be asking is about large deflection for which I thought would require:

$$ \frac{1}{\rho} = \frac{ \frac{d^2y}{dx^2}}{ \left( 1 + \left( \frac{dy}{dx}\right)^2 \right)^{(3/2)} } $$

 

[T1m0]

You can use the elementary beam theory equation d^2y/dx^2=-M/EI as long as the displacements are not too large (This case can be solved in closed form). How large is too large? - That tends to be problem dependent. As you indicated, the more complex expression for the beam radius of curvature would be required for "large" displacements. In that case you will probably have to solve the differential equation numerically.

 

[Juanda]

In your cantilever beam example, you did not get the internal bending moment quite right because you assumed that it was simply a linear function of x. I suggest that you get the moment by cutting the beam at some position x and drawing a free body diagram. This will lead to the following expression for moment

M(x)=-F_x*(y_B-y(x))-F_y*(L-x)

$$M(x)=-F_x*(y_B-y(x))-F_y*(L-x)$$
I think you're right on that. I assumed it was linear because of the following relations:
$$q(x)=\frac{dV}{dx}$$
$$V(x)=\frac{dM}{dx}$$
So with $q=0$ then M must be linear. Those equations are derived from making equilibrium in a differential size element.
NOTE: I used different letters to describe each term than what's shown in the picture.

However, making equilibrium in the deformed state and cutting it at $x$ I get an expression like yours.

This will give you a differential equation for y(x). Then solve the differential equation using the boundary conditions

At x=0, y=0
At x=0, dy/dx=0
At x=L, y=y_B

This is not too difficult, but the algebra gets messy.

Here I differ though. The third equation you propose isn't valid because it's not known. You might treat it as a constant but it still is an unknown constant.

Does $\frac{d^2y}{dx^2} = \frac{M(x)}{EI}$ even hold? What @Juanda seems to be asking is about large deflection for which I thought would require:

$$ \frac{1}{\rho} = \frac{ \frac{d^2y}{dx^2}}{ \left( 1 + \left( \frac{dy}{dx}\right)^2 \right)^{(3/2)} } $$

Agreed. But I also consider it best to try to solve it as simply as possible before introducing more complexity to the problem. Using that could be an interesting next step though.

You can use the elementary beam theory equation d^2y/dx^2=-M/EI as long as the displacements are not too large (This case can be solved in closed form). How large is too large? - That tends to be problem dependent. As you indicated, the more complex expression for the beam radius of curvature would be required for "large" displacements. In that case you will probably have to solve the differential equation numerically.

After what I posted on the boundary conditions. Do you still think it's solvable? If you think so, please share it. I don't see it.

 

[T1m0]

The solution of the differential equation is

y=C_1*sin(k*x)+C_2*cos(k*x)+C_3*x+C_4 where k=sqrt((F_x/(E*I)), C_3=-F_y/F_x, C_4=(F_x*y_B+F_y*L)/F_x

Use the three boundary conditions to solve for C_1, C_2, and y_B.

 

[Juanda]

The solution of the differential equation is

y=C_1*sin(k*x)+C_2*cos(k*x)+C_3*x+C_4 where k=sqrt((F_x/(E*I)), C_3=-F_y/F_x, C_4=(F_x*y_B+F_y*L)/F_x

Use the three boundary conditions to solve for C_1, C_2, and y_B.

The solution might be right. It looks a little like Euler's solution to buckling where trigonometric functions show up as well. I can't check the solution now though.
Still, my point remains. $y_B$ is NOT known. You can't use it for boundary conditions because it adds no information.
By the way, if you put your formulas between two $ they'll appear in LATEX format and centered. If you use two # instead they'll be in LATEX too but in line with the text.
For example:
$$y=C_1*sin(k*x)+C_2*cos(k*x)+C_3*x+C_4$$ where
$$k=sqrt((F_x/(E*I))$$ $$C_3=-F_y/F_x$$
$$C_4=(F_x*y_B+F_y*L)/F_x$$

 

[T1m0]

You can solve for y_B. Just crank through the algebra using the 3 boundary conditions. The third condition will give you an equation where y_B appears on both sides of the equation.

By the way, I am apparently too technology challenged to get Latex to work for me. That's why the equations appear in old school coding style.

 

[Juanda]

You can solve for y_B. Just crank through the algebra using the 3 boundary conditions. The third condition will give you an equation where y_B appears on both sides of the equation.

I think you're right once again. I wrote the equation in my notebook and then I could see it too.
It's too late for me to solve it now. Still, I'll try to do it over the weekend and plot $y(x)$ using the usual formulas and this case study which attempts to consider greater displacements by studying equilibrium in the deformed state.
The deformation must be greater because the bending moment on the beam is greater. It'll be interesting to see how different it is.

 

[Juanda]

I couldn't solve it analytically because the computer wouldn't let me (stack overflow for some reason). Inputting the expressions from @T1m0 felt like cheating so I solved it numerically.
I had to modify some signs here and there but the results make sense although I haven't figured out a way to check if they are really correct.

Here is the code

# -*- coding: utf-8 -*-
"""
Created on Sun Jul 21 21:47:24 2024

@author: Juanda
"""

import numpy as np
import matplotlib.pyplot as plt
from scipy.integrate import solve_ivp
from scipy.integrate import solve_bvp

# Units from International System
L = 1
E = 180e9
a = 50e-3
b = 50e-3
I = a**3*b/12

# Forces at B
F_x = -100000
F_y = -100

# "Normal" solution

# Reactions at A
R_x = -F_x
R_y = -F_y
MR_z = -F_y*L

# Define the bending moment function
def bending_moment(x):
    if 0 <= x <= L:
        return (MR_z * (L - x)) / L
    else:
        return 0

# Differential equation setup
# dy2/dx2 = -M(x) / (E * I)
def beam_deflection_eq(x, y):
    return [y[1], -bending_moment(x) / (E * I)]

# Initial conditions
y0 = [0, 0]  # Deflection and slope at x = 0

# Solve the differential equation numerically
sol_normal = solve_ivp(beam_deflection_eq, [0, L], y0, t_eval=np.linspace(0, L, 100))

# Extract solution
x_vals_normal = sol_normal.t
y_vals_normal = sol_normal.y[0]

# Bending moment function
def bending_moment_1(x, y, y_B):
    return F_x * (y_B - y) - F_y * (L - x)

# Differential equation setup
def beam_deflection_eq_1(x, y, p):
    y_B = p[0]
    return np.vstack((y[1], -bending_moment_1(x, y[0], y_B) / (E * I)))

# Boundary conditions
def boundary_conditions_1(ya, yb, p):
    y_B = p[0]
    return np.array([ya[0], ya[1], yb[0] - y_B])

# Initial guess for the solution
x_vals_bvp = np.linspace(0, L, 100)
y_initial = np.zeros((2, x_vals_bvp.size))

# Initial guess for y_B
y_B_guess = np.array([0.0])

# Solve the boundary value problem
sol_bvp = solve_bvp(beam_deflection_eq_1, boundary_conditions_1, x_vals_bvp, y_initial, p=y_B_guess)

# Check if the solver was successful
if sol_bvp.success:
    y_B = sol_normal.y[0,-1]
    y_B_1 = sol_bvp.p[0]
    y_vals_bvp = sol_bvp.sol(x_vals_bvp)[0]

    # Plotting the deflection curve
    plt.figure(figsize=(10, 6))
    plt.plot(x_vals_normal, y_vals_normal, label='Bernoulli Small Displacement', color='b')
    plt.plot(x_vals_bvp, y_vals_bvp, label='Bernoulli with small displacement but bending equilibrium once deformed', color='r', linestyle='--')
    plt.title('Beam Deflection Curve')
    plt.xlabel('Position along the beam (x) [m]')
    plt.ylabel('Deflection (y) [m]')
    plt.axhline(0, color='black', linewidth=0.5)
    plt.axvline(0, color='black', linewidth=0.5)
    plt.grid(color='gray', linestyle='--', linewidth=0.5)
    plt.legend()
    plt.show()

    print(f"Solved deflection with small displacements at x=L (y_B): {y_B}")
    print(f"Solved deflection with bending equilibrium once deformed at x=L (y_B): {y_B_1}")
else:
    print("Solver did not converge:", sol_bvp.message)

 

[T1m0]

Actually, there is a fairly simple analytical solution in Roark's Formulas for Stress and Strain book; i.e.,

y_B=(F_y/F_x)*(k*tan(L/k)-L) where k=sqrt(E*I/F_x)

 

[Juanda]

Actually, there is a fairly simple analytical solution in Roark's Formulas for Stress and Strain book; i.e.,

y_B=(F_y/F_x)*(k*tan(L/k)-L) where k=sqrt(E*I/F_x)

Could you tell me where you found it? I feel like that book contains everything but I never seem to be able to find what I'm looking for. And, if for any reason I find it, there are no explanations about it so I don't understand it.

By the way, I'm planning to add some graphs to this plot:

View attachment 348709

1. Deformation calculated "the normal way". This is using equilibrium in the undeformed state and Bernoulli with small deformations.
   $$M(x) = -F_y(L-x)$$
   $$M(x)=-EI\frac{d^2y}{dx^2}$$
   That's what's already shown in blue.
2. Deformation calculated with equilibrium in the deformed state (cutting the beam at $x$ to make a free body diagram as proposed by @T1m0 ) with Bernoulli and small deformations using a numerical solution.
   $$M(x)=F_x (y_B - y) - F_y (L - x)$$
   $$M(x)=-EI\frac{d^2y}{dx^2}$$
   Notice I had to change a sign in $M(x)$ with respect to what is shown in #12. Otherwise, the deflection was smaller than in the "normal" case. I assume it is because of some sign convention and the definition of the reference frame.
   That's what's already shown in red.
3. Deformation calculated with equilibrium in the deformed state (cutting the beam at $x$ to make a free body diagram) with Bernoulli and small deformations using the analytical solution to the differential equation and system of equations for the boundary conditions shown in #9 and #13 by @T1m0. If point 2 is correctly solved, it should yield the same solution.
   Pending.
4. Deformation calculated with equilibrium in the deformed state (cutting the beam at $x$ to make a free body diagram) with Bernoulli and small deformations using the analytical solution to the differential equation but using the information regarding the boundary conditions supplied by Roark's. Again, it'd give the same result as points 2 and 3.
   Pending.
5. If I still have some energy in me, I'll try to implement the large deformations as suggested by @erobz in #10.
   Pending.

 

[T1m0]

The solution in Roark's book can be found in the chapter on Beams in the section for "Beams under simultaneous axial compression and transverse loading." The complexity of the expression depends on which edition of the book that you have. The later editions are more difficult to decipher than the early ones.

Regarding sign conventions, most Mechanics of Materials books take the convention that positive internal bending moments are those that tend to make the beam "smile." When drawing the free body diagram for a cut section, always draw the moment going that way and let the moment equilibrium equation dictate the sign of the moment that is calculated. Next, equate this to the negative of the product of EI and the second derivative of displacement.

 

[Mishal0488]

As a structural engineer, I suggestion is to look into the finite element method. The stiffness matrix for beam elements is well defined and can easily be implemented using Python, Matlab, Julia etc... Furthermore Gridap presents an approach where the weak form of a differential equation can be used solve differential equations using the finite element method. https://github.com/gridap/Gridap.jl

 

[Juanda]

The solution in Roark's book can be found in the chapter on Beams in the section for "Beams under simultaneous axial compression and transverse loading." The complexity of the expression depends on which edition of the book that you have. The later editions are more difficult to decipher than the early ones.

Regarding sign conventions, most Mechanics of Materials books take the convention that positive internal bending moments are those that tend to make the beam "smile." When drawing the free body diagram for a cut section, always draw the moment going that way and let the moment equilibrium equation dictate the sign of the moment that is calculated. Next, equate this to the negative of the product of EI and the second derivative of displacement.

To be clear, are you referring to case 1a shown in table 8.8?
(Roark's Formulas for Stress and Strain 9th edition)

In that case, it's the right side the one that's fixed instead of the left one as I drew but I can mirror the results later. Also, to adapt it to our case I'd make $a=0$.
I am surprised by these formulas because the book must be doing something similar to what you showed (calculating the bending moment once deformed to find equilibrium). After all, the deflection would otherwise take a polynomial form but the book shows trigonometric functions.

I have a couple of questions on how to interpret what's shown in the formulas.

1. What's this operation $\left<x-a \right>^n$?
2. When it's saying $\cos k (l-a)$ it means this $\cos (k) * (l-a)$, right ?

 

[Juanda]

As a structural engineer, I suggestion is to look into the finite element method. The stiffness matrix for beam elements is well defined and can easily be implemented using Python, Matlab, Julia etc... Furthermore Gridap presents an approach where the weak form of a differential equation can be used solve differential equations using the finite element method. https://github.com/gridap/Gridap.jl

As far as I know, the stiffness matrix for beam elements only takes into account linear behavior which is applied for small displacements. At least that's the stiffness matrix for beams I know.
(Source)

That should provide the same results as what I showed here in blue.

View attachment 348709

To be precise, the stiffness matrix would only produce the results for the most left and most right nodes but the intermediate values can be found from that information. Anyway, the point is that, although the beam stiffness matrix is a very valuable concept, it's not the focus of this thread.


Note: The beam stiffness matrix I found during a quick search includes information on two degrees of freedom for each of the two nodes: vertical displacement (deflection) and angle. Axial displacement is ignored for the reasons explained in previous posts (it is considered irrelevant compared to the effect of bending). Isn't there a beam model that also accounts for the effect of axial loads?
I'm a little rusty, but I recall studying a beam stiffness matrix that includes the three degrees of freedom for each node within the plane: axial displacement, vertical displacement, and angle of deformation.
Such a matrix would also account for the effects of axial loads. I imagine that it's a matter of combining both displacements (adding them up), as they occur in perpendicular directions, resulting in the total displacement of the node. Intermediate values between the two nodes could be found in the same manner as previously mentioned.

 

[erobz]

I have a couple of questions on how to interpret what's shown in the formulas.

1. What's this operation $\left<x-a \right>^n$?

It's the singularity function.

https://eng.libretexts.org/Bookshel..._Deflection_by_Method_of_Singularity_Function

 

[Juanda]

It's the singularity function.

https://eng.libretexts.org/Bookshelves/Mechanical_Engineering/Introduction_to_Aerospace_Structures_and_Materials_(Alderliesten)/02:_Analysis_of_Statically_Determinate_Structures/07:_Deflection_of_Beams-_Geometric_Methods/7.04:_Deflection_by_Method_of_Singularity_Function

Thanks. Now that I read it I realize I have probably studied but I have to confess I completely forgot about it.
From the link:

In cases where a beam is subjected to a combination of distributed loads, concentrated loads, and moments, using the method of double integration to determine the deflections of such beams is really involving, since various segments of the beam are represented by several moment functions, and much computational efforts are required to find the constants of integration. Using the method of singularity function in such cases to determine deflections is comparatively easier and relatively quick.

I'm one of those guys taking the long route described by the text. I'll try to take the singularity function into account from now on since it is so convenient.

 

[Juanda]

It's the singularity function.

https://eng.libretexts.org/Bookshelves/Mechanical_Engineering/Introduction_to_Aerospace_Structures_and_Materials_(Alderliesten)/02:_Analysis_of_Statically_Determinate_Structures/07:_Deflection_of_Beams-_Geometric_Methods/7.04:_Deflection_by_Method_of_Singularity_Function

One last doubt about it though, what's then the point of making it $\left<x-a \right>^0$? For example, $F_{a1}$ contains an expression like that. With $0$ as an exponent, the result will either be $1$ which adds no value to a multiplication, or $0^0$ which is a problem in itself.

View attachment 349174

 

[erobz]

One last doubt about it though, what's then the point of making it $\left<x-a \right>^0$? For example, $F_{a1}$ contains an expression like that. With $0$ as an exponent, the result will either be $1$ which adds no value to a multiplication, or $0^0$ which is a problem in itself.

Its defined as $1$ for $x \geq a$ , and $0$ for $x<a$.

It pops up as useful in the shear equation. The example in my text is a simply supported beam, with a concentrated load $P$ at $L/2$.

The internal shear is $1/2 P$ when $x \leq L/2$, then it becomes $-1/2 P$ when $x > L/2$.

So you write the shear like:

$$ V(x) = \frac{1}{2}P - P\left< x - \frac{L}{2} \right>^0 $$

Integrating to get the bending moment:

$$ M(x) = \frac{1}{2}Px - P\left< x - \frac{L}{2} \right>^1 $$

And then you can carry on with the deflection integration.

 

[Juanda]

My bad. I read the definition of the function wrongly. I thought only what's withing the brackets changed to 0.
Clearly a sign it's bedtime for me. Thank you for the clarification.

 

[erobz]

My bad. I read the definition of the function wrongly. I thought only what's withing the brackets changed to 0.
Clearly a sign it's bedtime for me. Thank you for the clarification.

No worries I (obviously) had to look it up too.

 

[Juanda]

1. Deformation calculated "the normal way". This is using equilibrium in the undeformed state and Bernoulli with small deformations.
   $$M(x) = -F_y(L-x)$$
   $$M(x)=-EI\frac{d^2y}{dx^2}$$
   That's what's already shown in blue.
2. Deformation calculated with equilibrium in the deformed state (cutting the beam at $x$ to make a free body diagram as proposed by @T1m0 ) with Bernoulli and small deformations using a numerical solution.
   $$M(x)=F_x (y_B - y) - F_y (L - x)$$
   $$M(x)=-EI\frac{d^2y}{dx^2}$$
   Notice I had to change a sign in $M(x)$ with respect to what is shown in #12. Otherwise, the deflection was smaller than in the "normal" case. I assume it is because of some sign convention and the definition of the reference frame.
   That's what's already shown in red.
3. Deformation calculated with equilibrium in the deformed state (cutting the beam at $x$ to make a free body diagram) with Bernoulli and small deformations using the analytical solution to the differential equation and system of equations for the boundary conditions shown in #9 and #13 by @T1m0. If point 2 is correctly solved, it should yield the same solution.
   Pending.
4. Deformation calculated with equilibrium in the deformed state (cutting the beam at $x$ to make a free body diagram) with Bernoulli and small deformations using the analytical solution to the differential equation but using the information regarding the boundary conditions supplied by Roark's. Again, it'd give the same result as points 2 and 3.
   Pending.
5. If I still have some energy in me, I'll try to implement the large deformations as suggested by @erobz in #10.
   Pending.

I have calculated the vertical displacement of the node at the end using Roark's as mentioned in point 4 and it gives the same result as point 2 as expected. The difference in results is 6.283450322552842e-14 which comes down to the precision of the computer and the numerical approach used.
Point 3 I'd say is not relevant anymore.
Point 5 is still the one that could be interesting to invest some more time on it although I don't know how I'd do it now.

 

[Juanda]

@T1m0 you pretty much nailed the solution and even found it in Roark's which follows the same procedure you described in this thread. You gave me some hope back on tackling a similar problem. Let me introduce it and tell me if you'd be interested in giving it a whack.

For a while, I have been interested in knowing how pressurized tanks can be modeled with this kind of concept where the reactions depend on the deformation.
There are some similarities to the beam we've been discussing where the deformation causes the apparition of a torque that wasn't initially there. In pressurized tanks, the pressure makes it expand which increases the area where the pressure acts (assume pressure to be constant). So using equilibrium equations in the undeformed state is only an approximation. The actual deformation and stress will be greater just as what happened with the beam in this post.

I tried to tackle this problem already in this post but I got lost before understanding the matter. Do you know how to find a solution for such a situation?


EDIT.
Now that I think of it with the new perspective gained from this post I think this is how I'd do it.
Assuming there is a $k$ which relates the linear behavior between the pressure inside the tank and the radius, a constant pressure $P$, an area of the interior of the spherical tank $A$, the initial radius of the tank $r_i$ when there is no pressure and the actual radius $r$ when the pressure is applied:
$$PA=k(r-r_i)\rightarrow P(4\pi r^2)=k(r-r_i)$$
I don't know how to derive that $k$ now or if it's even linear so that might change but the overall procedure feels OK and in line with what we've been doing with the beam. That is, making equilibrium in the deformed state.
What do you think?

 

[Juanda]

EDIT.
Now that I think of it with the new perspective gained from this post I think this is how I'd do it.
Assuming there is a $k$ which relates the linear behavior between the pressure inside the tank and the radius, a constant pressure $P$, an area of the interior of the spherical tank $A$, the initial radius of the tank $r_i$ when there is no pressure and the actual radius $r$ when the pressure is applied:
$$PA=k(r-r_i)\rightarrow P(4\pi r^2)=k(r-r_i)$$
I don't know how to derive that $k$ now or if it's even linear so that might change but the overall procedure feels OK and in line with what we've been doing with the beam. That is, making equilibrium in the deformed state.
What do you think?

For greater clarity of what I'm trying to say, the "usual method" would be to make an equilibrium on the undeformed state. That would originate the following:
$$PA_i=k(r-r_i)\rightarrow P(4\pi r_i^2)=k(r-r_i)\rightarrow r=\frac{P(4\pi r_i^2)+kr_i}{k}$$
Using the equilibrium equation in the deformed state should yield greater deformation (and therefore, greater stress too).
$$PA=k(r-r_i)\rightarrow P(4\pi r^2)=k(r-r_i) \rightarrow 4P\pi r^2-kr+kr_i=0\rightarrow$$
$$\rightarrow r=\frac{-(-k) \pm \sqrt{(-k)^2-4(4P\pi)(kr_i)}}{2(4P\pi)}$$
I'm concerned by the fact that the result could be a complex number for certain input numbers which should be valid.
From the two solutions due to the square root, it seems the negative one is the correct one.
For as long as the second equation results in a real number, it's greater than the solution with the equilibrium in the undeformed state.
For smaller pressures, the results from the two equations are very close. As pressure increases, the results start to differ until the solution becomes a complex number which I don't understand how to interpret.
You can use this Desmos link to play around with the values if you want.

 

[T1m0]

Juanda, There is a Section in Roark's book on Thin Walled pressure vessels that gives a fairly simple formula for the radial expansion of a spherical tank as a function of internal pressure. The effect of this expansion on the pressure will strongly depend on whether the fluid inside the tank is a liquid or a gas. You can look at a number of websites regarding the topic of fluid compressibility; e.g.:

https://phys.libretexts.org/Bookshe...tatic_Fluids/27.5:_Compressibility_of_a_Fluid

 

[Juanda]

Juanda, There is a Section in Roark's book on Thin Walled pressure vessels that gives a fairly simple formula for the radial expansion of a spherical tank as a function of internal pressure.

Chapter 13. Shells of Revolution; Pressure Vessels; Pipes
It contains information about the spherical case which I believe is the simplest because of the present symmetries. However, the explanations are so concise that I can't make much out of them. It's a common problem I have with this book.
Still, one of the formulas shown there is related to what I'm trying to understand. To be precise:
$$\Delta R_2=\frac{qR_2^2(1-\nu)}{2Et}$$
The results will vary depending on whether

• we consider $R_2$ as the initial dimension which is known (the usual procedure) resulting in a linear result.

OR

• we consider $R_2$ the final dimension (what we have been discussing in the thread) resulting in a quadratic equation.

This is similar to what's shown in post #32 so the same questions remain.

 

[T1m0]

Juanda, you can find a fairly thorough explanation of the pressure vessel formulas in

https://pkel015.connect.amazon.auck...lasticity_Applications_03_Presure_Vessels.pdf

I am not aware of any analytical solutions to the pressure vessel problems for the large displacement case. This may be because most materials used in pressure vessels will experience yielding before the displacements get large. I suppose a really soft material might deform significantly before yielding. However, these materials tend to have more complicated stress-strain laws than Hooke's law.

In general, there are few analytical solutions to large displacement problems. The usual (and easiest) way to attack these problems is to use structural finite element analysis software (e.g., ANSYS, ABAQUS, etc). Although the full versions of these programs are very expensive, there are student versions that are free or very inexpensive.