Stationary observer meaning in relativity problem

[member 731016]

Homework Statement

Please see below

Relevant Equations

Please see below

For this problem,

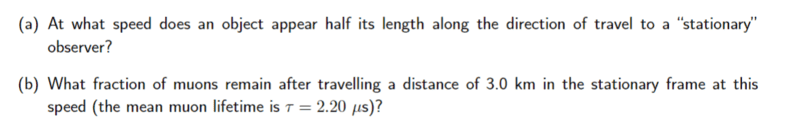
I don't understand what it means by the notation of a "stationary" observer. I thought there was no such thing as absolute rest. Does someone please know whether it means stationary with respect to the object?

Thanks!

 

[Orodruin]

Supposedly that’s why they put it in quotation marks. The intended meaning is most likely stationary in their rest frame, ie, the rest frame is inertial.

Note that there is no requirement that another physical object should be at rest in that frame.

 

[member 731016]

Supposedly that’s why they put it in quotation marks. The intended meaning is most likely stationary in their rest frame, ie, the rest frame is inertial.

Note that there is no requirement that another physical object should be at rest in that frame.

THank you for your reply @Orodruin!

Sorry I'm still confused by this problem. For (a) I get an imaginary velocity.

$L = \frac{L_0}{γ}$
$\frac{L_0}{2} = \frac{L_0}{γ}$
$2 = \sqrt{1 - \frac{v^2}{c^2}}$
$4 = 1 - \frac{v^2}{c^2}$
$3 = -\frac{v^2}{c^2}$
$\sqrt{-3c^2} = v$

Thanks!

 

[Hill]

THank you for your reply @Orodruin!

Sorry I'm still confused by this problem. For (a) I get an imaginary velocity.

$L = \frac{L_0}{γ}$
$\frac{L_0}{2} = \frac{L_0}{γ}$
$2 = \sqrt{1 - \frac{v^2}{c^2}}$
$4 = 1 - \frac{v^2}{c^2}$
$3 = -\frac{v^2}{c^2}$
$\sqrt{-3c^2} = v$

Thanks!

Check the line 3.

 

[member 731016]

Check the line 3.

Thank you for your reply @Hill!

I have checked it, and it looks correct to me. I just flipped both of the fractions up and bottom which is allowed please?

Thanks!

 

[Hill]

Thank you for your reply @Hill!

I have checked it, and it looks correct to me. I just flipped both of the fractions up and bottom which is allowed please?

Thanks!

No, it is not correct. Show your steps.

 

[member 731016]

No, it is not correct. Show your steps.

Thank you for your reply @Hill!

That is my steps. That is the steps wrote down when solving the problem. Basically be law of algebra, if I flip one side I can flip the other right?

Thanks!

 

[Hill]

Thank you for your reply @Hill!

That is my steps. That is the steps wrote down when solving the problem. Basically be law of algebra, if I flip one side I can flip the other right?

Thanks!

Yes, you can flip. But this flipping does not produce your line 3 shown above.

 

[member 731016]

Yes, you can flip. But this flipping does not produce your line 3 shown above.

Thank you for you reply @Hill! Sorry I'm so confused.The $L_0$s both cancel, do you please know what I am missing?

Thanks!

 

[Hill]

Thank you for you reply @Hill! Sorry I'm so confused.The $L_0$s both cancel, do you please know what I am missing?

Thanks!

Can you show how you get $2 = \sqrt{1 - \frac{v^2}{c^2}}$? Not with words, only with algebra.

 

[member 731016]

Can you show how you get $2 = \sqrt{1 - \frac{v^2}{c^2}}$? Not with words, only with algebra.

Thank you for your reply @Hill!

No I can't sorry, it is something I learnt many years ago, I just know from the law of algebra if you do one thing to one side then you need to do the same thing to the other side. Do you please know the steps?

Thanks!

 

[Hill]

Thank you for your reply @Hill!

No I can't sorry, it is something I learnt many years ago, I just know from the law of algebra if you do one thing to one side then you need to do the same thing to the other side. Do you please know the steps?

Thanks!

When you flip $\frac{L_0}{2} = \frac{L_0}{γ}$, you get $2 = γ$. It is not the same as $2 = \sqrt{1 - \frac{v^2}{c^2}}$.

 

[member 731016]

When you flip $\frac{L_0}{2} = \frac{L_0}{γ}$, you get $2 = γ$. It is not the same as $2 = \sqrt{1 - \frac{v^2}{c^2}}$.

Oh thank you @Hill! Sorry I did't see that. That should fix the sign error then.

Thanks!

 

[Hill]

Oh thank you @Hill! Sorry I did't see that. That should fix the sign error then.

Thanks!

Do NOT jump steps in algebra!

 

[member 731016]

Do NOT jump steps in algebra!

Thank you for your reply @Hill! Sorry I did't consider that jump steps in agelbra. This is what trying to do SR on 2 hours of sleep does to my brain