Statistical Mechanics: Cooling to Bose-Einstein condensate

[Decimal]

Hello,

I have a question regarding the derivation for Bose Einstein condensation. I understand that in a boson gas for high temperatures the expectation value of the total number of particles should equal something like: $$ \langle N \rangle \sim T * \eta(z)$$ With $z = exp(\frac {\mu} {k_b T})$, $T$ the temperature and $$ \eta(z) = \int_0^\infty \frac{x^2}{z^{-1}*exp(x)-1} \, dx$$ This function $\eta(z)$ increases for decreasing $z$ until it reaches a maximum at $z = 1$. The graph looks like this:

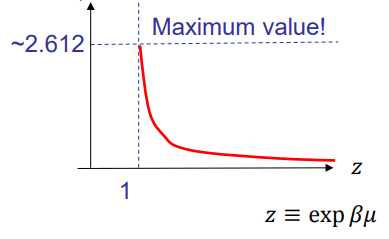
Now if I understand correctly, what you want to do is start cooling the system whilst keeping the number of particles constant. My question is, how? If you decrease $T$ then $z$ will increase thus lowering the value of $\eta(z)$. Because of this the number of particles should always decrease right? I feel like I am missing something here so maybe someone could explain?

Thanks!

Edit: So I feel like I should clarify a couple of things. The above expression for $\langle N \rangle$ gives the number of particles in the excited state. In other words, all particles except the ones in the ground state. Now my lecture notes explain that one can lower the temperature whilst keeping the number of particles (in excited states) constant, up until the $\eta(z)$ maxes out at $z=1$. After this point particles will start to move to the ground state which defines the critical temperature. I understand this, but still don't see how the number of particles can be held constant at all. Lowering $T$ also lowers $\eta(z)$ so number of particles will never be held constant right? Lowering the temperature immediately lowers the number of particles in the excited states.

 

[eljose79]

Hello,

Thank you for your question. You are correct in your understanding that for a boson gas at high temperatures, the expectation value of the total number of particles can be approximated by $$ \langle N \rangle \sim T * \eta(z)$$ with $z = exp(\frac {\mu} {k_b T})$. As you mentioned, this function $\eta(z)$ increases for decreasing $z$ until it reaches a maximum at $z = 1$.

In order to understand how the number of particles can be held constant while lowering the temperature, it is important to consider the concept of chemical potential. The chemical potential, denoted by $\mu$, is a measure of the energy required to add one particle to the system. It is related to the temperature and number of particles by the equation $\mu = k_b T * ln(\frac{\langle N \rangle}{N_0})$, where $N_0$ is the number of particles in the ground state.

When the temperature is lowered, the chemical potential also decreases. This means that the energy required to add a particle to the system decreases, making it easier for particles to move into the excited states. In this way, the number of particles in the excited states can remain constant even as the temperature is lowered. Once the temperature reaches the critical temperature, the chemical potential becomes equal to the energy of the ground state, and particles begin to move into the ground state, resulting in the observed Bose Einstein condensation.

I hope this helps to clarify your question. If you have any further questions, please let me know.