- #1
EricTheWizard
- 14
- 0
Hi everyone, I've hit a bit of a snag with part c of this problem (can't figure out how to invert a function T(ν)), so I'm starting to question whether I have the previous parts correct.
Consider a system of N identical but distinguishable particles, each of which has a
nondegenerate ground state with energy zero, and a g-fold degenerate excited state with
energy ε > 0.
(a) Let the total energy of the system be fixed at E = Mε, where M is the number of
particles in an excited state. What is the total number of states (E,N)?
(b) What is the entropy S(E,N)? Assume the system is thermodynamically large. You
may find it convenient to define ν ≡ M/N, which is the fraction of particles in an
excited state.
(c) Find the temperature T(ν). Invert this relation to find ν(T).
(d) Show that there is a region where the temperature is negative.
(e) What happens when a system at negative temperature is placed in thermal contact
with a heat bath at positive temperature?
entropy: S(E,N) = k \ln \Omega (E,N), where \Omega is the number of states with energy E and particle number N.
temperature: \frac{1}{T} = (\frac{\partial{S}}{\partial{E}})_{V,N}
Stirling's approximation: k! ≈ \sqrt{2\pi k}e^{-k}k^{k}
a) A particle can be in either the ground state or one of g excited states, so the number of states with excited particle number M should be \Omega(M,N) = {{N}\choose{M}} g^M because there are {N}\choose{M} ways to arrange which particles in an ensemble are excited, and then g choices for each particle of which degenerate state they're in. This seems to make sense to me, anyways.
b) To find the entropy, simply take the natural logarithm of Ω (which requires you to make Stirling's approximation so that you can pull parts of the factorials through the log)
S = k \ln\Omega ≈ k \ln{(\frac{N^{N+1/2}g^M}{\sqrt{2\pi}(N-M)^{N-M+1/2}M^{M+1/2}})} = k[(N+1/2)\ln N + \frac{E}{\epsilon}\ln g - \frac{1}{2}\ln(2\pi)-(N-\frac{E}{\epsilon}+\frac{1}{2})\ln{(N-\frac{E}{\epsilon})}-(\frac{E}{\epsilon}+\frac{1}{2})\ln{\frac{E}{ε}} ]
c) Now find the temperature distribution T(\nu) making the substitution \nu = M/N = E/N\epsilon, the fraction of particles in the excited state and using the formula for temperature given above.
\frac{1}{T} = \frac{\partial S}{\partial E} = \frac{k}{\epsilon}[\ln g + \ln(N - E/\epsilon) + \frac{N-E/\epsilon+1/2}{N-E/\epsilon}-\ln\frac{E}{\epsilon}-(1-\frac{\epsilon}{2E})] = \frac{k}{\epsilon}[\ln\frac{g(1-\nu)}{\nu}+\frac{1}{2N}\frac{2\nu-1}{\nu (1-\nu)}] = \frac{1}{T(\nu)}
Now this is the part I'm stuck at; I simply can't invert T(ν) because it's not a 1-to-1 function. If you plot it in Mathematica or similar, you get something like this:
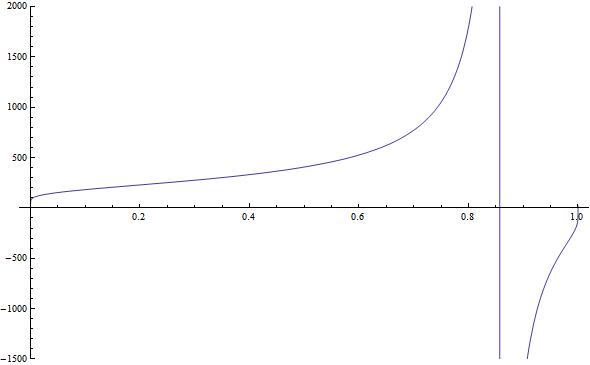
which (and you can't see this very well) turns downward near ν=1 very sharply and makes the distribution non-invertible (at least in the negative temperature zone). Have I made a mistake somewhere?
d) Set T<0 and solve for the pertinent conditions (haven't tried this yet)
e) Heat will flow from a negative temperature system to a positive temperature one if they come in contact.
Homework Statement
Consider a system of N identical but distinguishable particles, each of which has a
nondegenerate ground state with energy zero, and a g-fold degenerate excited state with
energy ε > 0.
(a) Let the total energy of the system be fixed at E = Mε, where M is the number of
particles in an excited state. What is the total number of states (E,N)?
(b) What is the entropy S(E,N)? Assume the system is thermodynamically large. You
may find it convenient to define ν ≡ M/N, which is the fraction of particles in an
excited state.
(c) Find the temperature T(ν). Invert this relation to find ν(T).
(d) Show that there is a region where the temperature is negative.
(e) What happens when a system at negative temperature is placed in thermal contact
with a heat bath at positive temperature?
Homework Equations
entropy: S(E,N) = k \ln \Omega (E,N), where \Omega is the number of states with energy E and particle number N.
temperature: \frac{1}{T} = (\frac{\partial{S}}{\partial{E}})_{V,N}
Stirling's approximation: k! ≈ \sqrt{2\pi k}e^{-k}k^{k}
The Attempt at a Solution
a) A particle can be in either the ground state or one of g excited states, so the number of states with excited particle number M should be \Omega(M,N) = {{N}\choose{M}} g^M because there are {N}\choose{M} ways to arrange which particles in an ensemble are excited, and then g choices for each particle of which degenerate state they're in. This seems to make sense to me, anyways.
b) To find the entropy, simply take the natural logarithm of Ω (which requires you to make Stirling's approximation so that you can pull parts of the factorials through the log)
S = k \ln\Omega ≈ k \ln{(\frac{N^{N+1/2}g^M}{\sqrt{2\pi}(N-M)^{N-M+1/2}M^{M+1/2}})} = k[(N+1/2)\ln N + \frac{E}{\epsilon}\ln g - \frac{1}{2}\ln(2\pi)-(N-\frac{E}{\epsilon}+\frac{1}{2})\ln{(N-\frac{E}{\epsilon})}-(\frac{E}{\epsilon}+\frac{1}{2})\ln{\frac{E}{ε}} ]
c) Now find the temperature distribution T(\nu) making the substitution \nu = M/N = E/N\epsilon, the fraction of particles in the excited state and using the formula for temperature given above.
\frac{1}{T} = \frac{\partial S}{\partial E} = \frac{k}{\epsilon}[\ln g + \ln(N - E/\epsilon) + \frac{N-E/\epsilon+1/2}{N-E/\epsilon}-\ln\frac{E}{\epsilon}-(1-\frac{\epsilon}{2E})] = \frac{k}{\epsilon}[\ln\frac{g(1-\nu)}{\nu}+\frac{1}{2N}\frac{2\nu-1}{\nu (1-\nu)}] = \frac{1}{T(\nu)}
Now this is the part I'm stuck at; I simply can't invert T(ν) because it's not a 1-to-1 function. If you plot it in Mathematica or similar, you get something like this:
which (and you can't see this very well) turns downward near ν=1 very sharply and makes the distribution non-invertible (at least in the negative temperature zone). Have I made a mistake somewhere?
d) Set T<0 and solve for the pertinent conditions (haven't tried this yet)
e) Heat will flow from a negative temperature system to a positive temperature one if they come in contact.