- #1
MarcL
- 170
- 2
Sorry if this is in the wrong section. I didn't know which homework section I should use.
1. Homework Statement
Human subjects are involved in a medical study to represent certain segments of the population in terms of blood lead concentration, PbB. First, assume the normal distribution properly represents the population of children with the mean concentration of 22.5 μg/dl and the standard deviation σ of 5.8 μg/dl. Then, determine the range of PbB values (minimum and maximum) that should be used for the top 3 % of PbB values in the population. Use the cumulative density function table provided.
here's the table:
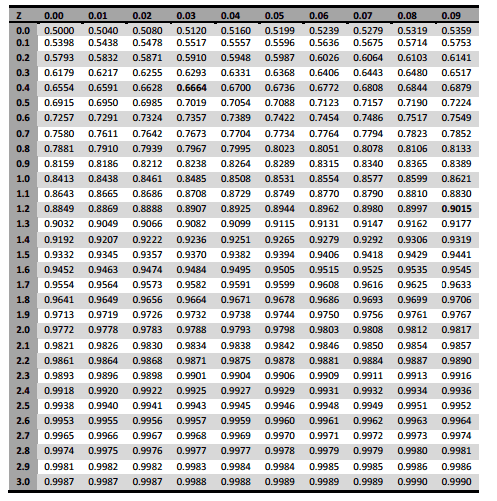
Also z = (X - μ) / σ where μ is the mean and σ is the standrad deviation.
I'm not too sure on what I did... might be completely off. I used the following logic. If it is the top 3%, then we can find the maximum density using 0% as our total. Therefore, we would need to have Z = 3.9 on both side of the probability ( by that I mean P( 3.9 < Z < 3.9) ). So using that idea, we can find Xmax using the following:
3.9 = (X - 22.5) /5.8 --> 45.15 ug/dl
For the the Xmin , also the lost integer in the interval, I used the following:
φ(z=3.9) - φ(z= y ) = .03 --> .9999 - y = .03 --> y=.9699
Therefore, using the table .9699 will give you 1.88.
Using the same method as above, 1.88 will give x as 33.40 ug/dl
This whole thing seems completely wrong though. I've never taken a stat class before and this was handed to me. Using the best of my abilities ( and wikipedia) to try to understand.
1. Homework Statement
Human subjects are involved in a medical study to represent certain segments of the population in terms of blood lead concentration, PbB. First, assume the normal distribution properly represents the population of children with the mean concentration of 22.5 μg/dl and the standard deviation σ of 5.8 μg/dl. Then, determine the range of PbB values (minimum and maximum) that should be used for the top 3 % of PbB values in the population. Use the cumulative density function table provided.
Homework Equations
here's the table:
Also z = (X - μ) / σ where μ is the mean and σ is the standrad deviation.
The Attempt at a Solution
I'm not too sure on what I did... might be completely off. I used the following logic. If it is the top 3%, then we can find the maximum density using 0% as our total. Therefore, we would need to have Z = 3.9 on both side of the probability ( by that I mean P( 3.9 < Z < 3.9) ). So using that idea, we can find Xmax using the following:
3.9 = (X - 22.5) /5.8 --> 45.15 ug/dl
For the the Xmin , also the lost integer in the interval, I used the following:
φ(z=3.9) - φ(z= y ) = .03 --> .9999 - y = .03 --> y=.9699
Therefore, using the table .9699 will give you 1.88.
Using the same method as above, 1.88 will give x as 33.40 ug/dl
This whole thing seems completely wrong though. I've never taken a stat class before and this was handed to me. Using the best of my abilities ( and wikipedia) to try to understand.