Steel Angle Plastic Section Modulus

[Engineering01]

Hi all,

I am after trying to find the plastic section modulus about both local axes (x & y) after having calculated them for the global axes (n & p). Is there a way I can transform global to local using Morh’s circle to evaluate plastic section properties?

Attached is the key diagram I am working to:

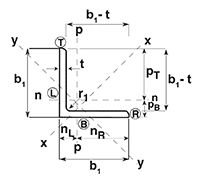
I have been able to evaluate all other section properties locally and globally except for the local plastic section modulus about the x and y axes. I want to avoid going back to first principals in evaluating the plastic section modulus about the rotated local axes because they may cut through the fillets (r1 & r2) which will really complicate things.

Any advice would be greatly appreciated.

 

[SteamKing]

I'm not aware of any such transformation. Either ignore the fillets or square them off. After all, in tabulating elastic properties, especially in the AISC tables, these fillets for angles are ignored anyway.