- #1
bulldog23
- 120
- 0
[SOLVED] collision problem
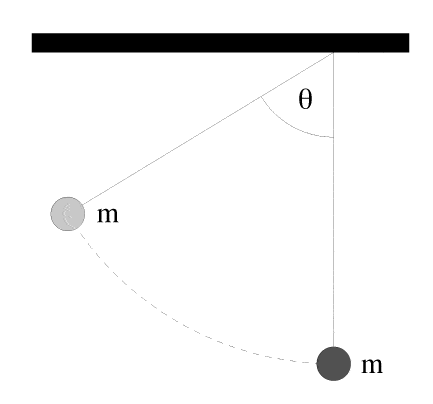
Two identical steel balls, each of mass 3.4 kg, are suspended from strings of length 27 cm so that they touch when in their equilibrium position. We pull one of the balls back until its string makes an angle theta = 74o with the vertical and let it go. It collides elastically with the other ball.
A) How high will the other ball rise above its starting point?
B)Suppose that instead of steel balls we use putty balls. They will collide inelastically and remain stuck together after the collision. How high will the balls rise after the collision?
P=m*v
m1v1=m2v2
I am unsure how to start this problem. I know that the total initial momentum must equal the total final momentum, because the collision is elastic. Can someone help me out by explaining part A and part B?
Homework Statement
Two identical steel balls, each of mass 3.4 kg, are suspended from strings of length 27 cm so that they touch when in their equilibrium position. We pull one of the balls back until its string makes an angle theta = 74o with the vertical and let it go. It collides elastically with the other ball.
A) How high will the other ball rise above its starting point?
B)Suppose that instead of steel balls we use putty balls. They will collide inelastically and remain stuck together after the collision. How high will the balls rise after the collision?
Homework Equations
P=m*v
m1v1=m2v2
The Attempt at a Solution
I am unsure how to start this problem. I know that the total initial momentum must equal the total final momentum, because the collision is elastic. Can someone help me out by explaining part A and part B?