Stiffness Matrix For a Beam

[Zouatine]

TL;DR Summary

u(x)=(1-x/l)*u1+(x/l)*u2 Horizontal displacement
w(x)=(1-x/l)*w1+(x/l)*w2 Vertical displacement

hello
i hope everyone doing well,
I have problem in Stiffness Matrix For Beam element (2 nodes )
i have a beam element i want to get a stiffness matrix:
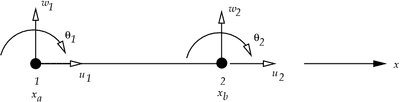
we have beam element (2 nodes)
node (1) : u1 horizontal displacement, v1 vertical displacement
node (2): u2 horizontal displacement , v2 vertical displacement
i know that the stiffness matrix is the relation between the forces in nodes and displacement
ke : Stiffness Matrix
D: displacement
F : forces
N : shape function

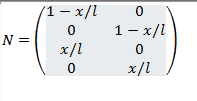
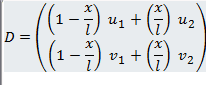rotation are 0 .
stiffness matrix will be

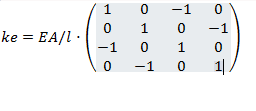
i want to know if the sttifnes matrix is correct if not how can I get the correct one ?

thank you

 

[Navin A S]

The stiffness matrix for a beam element with two nodes is given by: K = [k11 k12; k21 k22]where, k11 = EA/Lk12 = -EA/Lk21 = -EA/Lk22 = EA/LE is the Young's modulus of the material and A is the area of the cross section of the beam. L is the length of the beam between the two nodes. Thus, the stiffness matrix for a beam element with two nodes can be expressed as: K = [EA/L -EA/L; -EA/L EA/L]