WMDhamnekar
MHB
- 376
- 28
- Homework Statement
- Suppose ##X_1,X_2 \dots ## are independent random variables with ##\mathbb{P}[X_j= 1] =1- \mathbb{P}[X_j=-1]=\frac13## Let ## S_n = X_1 +\dots +X_n## Find ## \mathbb{E}[S_n], \mathbb{E}[S^2_n], \mathbb{E}[S^3_n]##
- Relevant Equations
- Not applicable
Are my following answers correct?
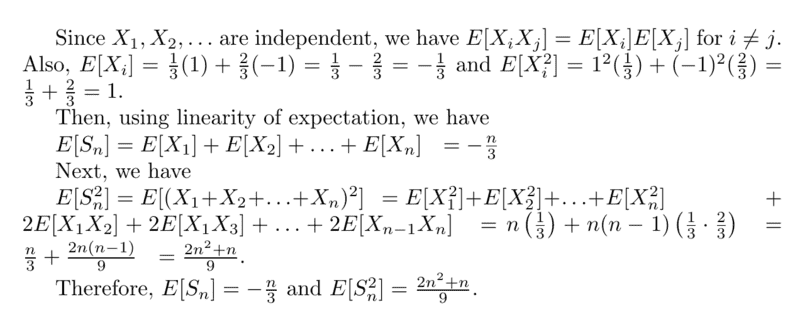

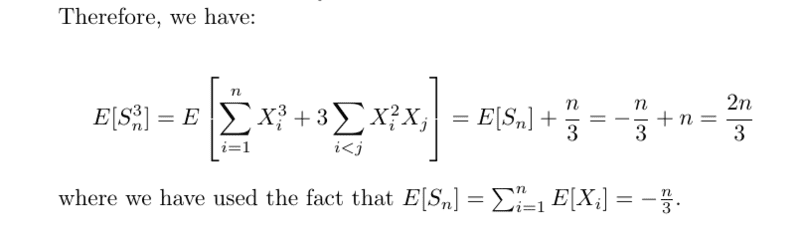
Last edited: