Straight Current Carrying Wires and Magnetic Field

[Sudharshan]

Homework Statement

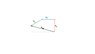
Three straight current carrying wires for each a current I as shown below. They are in the corners of a square that has sides a. Specify the resulting magnetic field at point P in the lower right corner, give both size and direction of the field.

Homework Equations

Magnetic Field B = (μ₀I)/(2∏r)
r = distance
I = current

The Attempt at a Solution

I have a finished answer to the question but I am not sure if it correct. I have linked a picture of my solution below.
http://i.imgur.com/UUx4C8M.jpg

I am not sure if i have calculated B_z correctly. Is the B_z that I have calculated correct? Is rest of the solution correct?

Any Help is Appreciated.

 

[Tanya Sharma]

Hi Sudarshan...

Welcome to PF!

You have calculated separate magnetic fields due to the three wires correctly . But the net magnetic field is incorrect .

You need to find the net magnetic field by adding the individual magnetic fields as vectors not as scalars .

 

[Sudharshan]

Hi Sudarshan...

Welcome to PF!

You have calculated separate magnetic fields due to the three wires correctly . But the net magnetic field is incorrect .

You need to find the net magnetic field by adding the individual magnetic fields as vectors not as scalars .

Hey Tanya!

Thanks for your quick reply. Does this mean that my B_z is correct? I mean the part where I multiply by Tanθ. I thought this part (multiply by cos or sin or tan) was where the direction of the fields came into play? I don't understand the part about adding them as vectors. I calculated that the total magnetic field direction was to the left (towards wire z) by vector addition as shown on my answer sheet (top right corner with the arrows). The same with the magnitude. Are they wrong? Can you please explain further. Thank you.

 

[Tanya Sharma]

The direction of magnetic field due to top left wire at point P is 45° below the horizontal .
The direction of magnetic field due to top right wire at point P is towards left .
The direction of magnetic field due to bottom left wire at point P is upwards .

Do you agree with this ?

 

[Sudharshan]

Yes. I agree.
For top left wire, I multiplied with cos(45).
For top right wire, I multiplied with nothing cause its field is the direction of total field.
For bottom left wire, I multiplied with tan(45).

 

[Tanya Sharma]

Well...in order to find the direction of magnetic fields due to individual wires,there is no need to multiply by cos45 or tan45 .

Suppose there is only one wire ,z,the magnetic field lines around that wire are concentric circles with z at the center.The direction at any point P is given by a tangent to the circle at P .In our case it points upwards .

For y,the magnetic field lines around that wire are concentric circles with y at the center.The direction at any point P is given by a tangent to the circle at P .In our case it points leftwards .

Look at the illustration here http://hyperphysics.phy-astr.gsu.edu/hbase/magnetic/magcur.html

 

[Tanya Sharma]

I don't understand the part about adding them as vectors. I calculated that the total magnetic field direction was to the left (towards wire z) by vector addition as shown on my answer sheet (top right corner with the arrows).

You have added them incorrectly .The resultant vector doesn't point towards left .

Look at the attachment .Here I have made the three vectors .The resultant is in black ,making an angle with the horizontal.

 

[Sudharshan]

Hey Tanya,

After looking through the website that you have linked and the vector drawing that you made, I think I have calculated the correct answer. I have linked it below. Is this the correct solution? Both magnitude and direction?

http://i.imgur.com/Gppdu3r.jpg

 

[Tanya Sharma]

Hey Tanya,

After looking through the website that you have linked and the vector drawing that you made, I think I have calculated the correct answer. I have linked it below. Is this the correct solution? Both magnitude and direction?

http://i.imgur.com/Gppdu3r.jpg

You don't seem to be comfortable with vector addition .That is not how vectors are added .You seem to add them algebraically .

Here is a reference http://hyperphysics.phy-astr.gsu.edu/hbase/vect.html

Set up your coordinate system with origin at P and positive x-axis leftwards and y-axis upwards .

Look at the attachment.

Here

The magnetic field due to top left wire at point P is B1(green).
The direction of magnetic field due to top right wire is B2(blue) .
The direction of magnetic field due to bottom left wire is B3(red) .

Decompose these vectors along the coordinate axes .

B1 will have a component in both x and y directions (B_1x and B_1y) .
B2 has component in only x direction.
B3 has component in only y direction .

Add all the components in x direction taking care of the signs.This will give you the component of net magnetic field in x direction . Let us call this H_x.

Add all the components in y direction taking care of the signs.This will give you the component of net magnetic field in y direction . Let us call this H_y.

The magnitude of the net magnetic field H will be = √(H_x²+H_y²) .

H makes an angle θ with the x-axis given by θ = tan^-1(H_y/H_x)

 

[Sudharshan]

Hey Tanya,

Thanks for taking the time to help me with this problem. I completely forgot about vector additions and the way to calculate them even though I studied them in high school xD. The website you linked was very educational.

I have now calculated the total magnetic field by splitting it up into components as you suggested. I have also calculated the angle θ. It would be great if you could take a look and tell me if I have made any mistakes, especially when I am calculating the magnitude of B and B_y

Page 1: http://i.imgur.com/IEtjXPu.jpg

Page 2: http://i.imgur.com/uuCxoxY.jpg

 

[Tanya Sharma]

Just a minor correction ,θ = 18.3°

Except that ,well done :thumbs:

 

[Sudharshan]

Thanks again for all your help Tanya.

 

[Tanya Sharma]

You are welcome