Strange question — Catapult launching a marble over an obstacle

[neilparker62]

Homework Statement

Am I seeing "gremlins" where there aren't any or is there something odd about this question ? In 3c), how can you calculate how long it takes to "clear" an obstacle if the width of the obstacle is not known? Nor the horizontal velocity of the projectile.

Relevant Equations

s=ut + 1/2 a t^2

[Attachment edited for clarity by the Mentors]

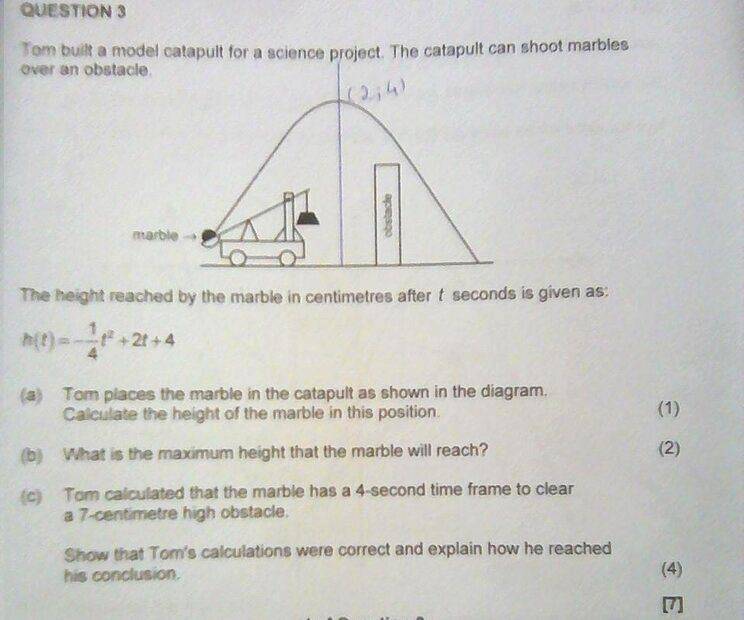
https://www.physicsforums.com/attachments/284341

 

[Delta2]

I am not sure how exactly to interpret (c), however when I solve the equation $h(t)=7$ I get two values for t, namely $t_1=2$ and $t_2=6$ and it is $t_2-t_1=4$ (equal to the 4-second time frame) .

It is also $h(t)>7$ for $t_1<t<t_2$.

I guess by "time frame to clean an obstacle of height 7cm" it means the width of the time interval $I$ such that $h(t)\geq 7$ for every $t\in I$.

 

[neilparker62]

I am not sure how exactly to interpret (c), however when I solve the equation $h(t)=7$ I get two values for t, namely $t_1=2$ and $t_2=6$ and it is $t_2-t_1=4$ (equal to the 4-second time frame) .

It is also $h(t)>7$ for $t_1<t<t_2$.

I guess by "time frame to clean an obstacle of height 7cm" it means the width of the time interval $I$ such that $h(t)\geq 7$ for every $t\in I$.

Yes if they just asked something like "for what length of time is the marble above 7cm in height" it would be fine. But the picture of an apparently thin object and wording "time frame to clear" just don't make any physical sense.

 

[kuruman]

Using the given equation, Tom calculates that the projectile is above 7 units in the time interval $2 ~\text{s} \leq t \leq 6~ \text{s}.$
Using the given equation, Tom calculates that the projectile returns to the initial height of 4 units at t = 8 s.
Using his noggin, Tom figures that: 2 s are needed to reach the near edge, 2 s are needed to come back down, which leaves no more than 4 s to fly above the obstacle.
Yay, Tom!

 

[neilparker62]

Using the given equation, Tom calculates that the projectile is above 7 units in the time interval $2 ~\text{s} \leq t \leq 6~ \text{s}.$
Using the given equation, Tom calculates that the projectile returns to the initial height of 4 units at t = 8 s.
Using his noggin, Tom figures that: 2 s are needed to reach the near edge, 2 s are needed to come back down, which leaves no more than 4 s to fly above the obstacle.
Yay, Tom!

The problem for Tom was that he was not advised how thick the obstacle was. Perhaps it was the thinnest of thin plates. Then as long as it was appropriately placed such that the catapaulted marble was above 7cm by the time it 'reached' the plate, it would clear it in an undefined trice ! Tom's calculation is based on the premise that the obstacle is 7cm high and exactly 4 seconds "wide" at whatever unspecified horizontal velocity the marble was fired at. But personally I very much doubt that Tom's creator gave that a moment's thought!

 

[kuruman]

Tom's calculation is based on the premise that the obstacle is 7cm high and exactly 4 seconds "wide" at whatever unspecified horizontal velocity the marble was fired at.

That's not how I read the problem. Tom is given a formula and a 7-cm high barrier. There is no language in the problem that says that the barrier is exactly 4 s wide. Rather, Tom has done the calculation and claims that, as long as the barrier is less than 4 s wide, a distance to it can always be found such that the marble will clear the obstacle. We are asked to substantiate this claim. Furthermore, the accompanying figure shows that, at barrier height, the parabolic trajectory is several times as wide as the barrier.

 

[neilparker62]

Ok statement 1 holds: I saw gremlins where there aren't any!

 

[kuruman]

No gremlins. Tom can even calculate the maximum width of the obstacle that will allow an uninterrupted flyover and the horizontal distance from the wall where the marble should start.

The given equation $h(t) = -\frac{1}{4}t^2+2t+4$ implies $h_0=4$ cm, $v_{0y}=2$ cm/s and $g=\frac{1}{2}$ cm/s². The units are specified in the problem therefore we must conclude that Tom is not near the Earth's surface.

This says that in the 2 s the marble rises to the height of 7 cm, its vertical velocity is reduced from 2 cm/s to 1 cm/s. At that point, to maximize the horizontal range, the local projection angle must be 45^o. This means that $v_{0x}=1$ cm/s which means that the maximum width must be 4 cm and that the marble must be shot from a distance of 2 cm from the obstacle. The initial projection angle is $\theta=\arctan(\frac{2}{1})=$ 63.4^o.

 

[neilparker62]

All good but re the "gremlin" , let me pose my original question slightly differently.

Suppose the obstacle were 1mm thick. Would the marble still require a 4 second time frame to clear said obstacle ? I think the "gremlin" is in one's interpretation of "time frame to clear" which could arguably refer to the time it takes the marble to move across the article rather than the entire time frame for which the marble's height is above 7cm.

Setting a test is not about clever 'trip-wire' type wording. It's about wording problems in a way which enables students to show what they do know rather than what they don't. If we want students to show they can solve a quadratic inequality correctly, the obvious wording is "find the time for which the marble is above a height of 7cm". The more so when alternate "clever stuff" wording ends up being ambiguous at least to my (admittedly gremlin prone!) ear.

 

[kuruman]

I agree with you that problem statements must be unambiguously stated. Authoring problems requires anticipation of possible misinterpretations by the reader whose native language may not necessarily be English in some cases.

I also object to the disregard for realistic numbers in some cases. I believe that when numbers are given, they ought to be more or less realistic because part of the training is having a sense of what constitutes a reasonable number. It is unreasonable for a correct answer to have a car passing another car in a city street at a speed of 80 m/s. Here it is unreasonable to have an acceleration of gravity of 1/2 cm/s². A back-of-the-envelope calculation shows that Tom must be on an asteroid of radius 1 mile, assuming that the asteroid is spherical and has the same average mass density as the Earth. Of course, I understand that this is probably some kind of standard test problem that bans calculators and therefore the numbers must be simple. Oh well.

 

[rsk]

Just my tuppenceworth

The problem might not seem clearly stated but I think that may be either intentional and the reason for the "explain how he reached his solution" bit.
I initially assumed I was looking for the total time to return to 7cm of height but when the quadratic gave answers 4s apart, realized that's what he had done.

Whatever the thickness of the barrier (or the horizontal cmpt of velocity), the marble has 4 seconds when it can clear that height.

 

[neilparker62]

Just my tuppenceworth

The problem might not seem clearly stated but I think that may be either intentional and the reason for the "explain how he reached his solution" bit.
I initially assumed I was looking for the total time to return to 7cm of height but when the quadratic gave answers 4s apart, realized that's what he had done.

Whatever the thickness of the barrier (or the horizontal cmpt of velocity), the marble has 4 seconds when it can clear that height.

Thanks for the comment - I'm just very sensitive (low "gremlin threshold"!) to question wording that (to quote you) "might not seem clearly stated". Students of mine really do put in intensive effort and it's very galling when they get poor marks on assessments because they haven't been able to decipher the wording. A critical component of tuition (to my mind) is getting students into a place where they do well on their assessments, get positive reinforcement, are further motivated etc. That's why I think there's a big responsibility on assessors and they need to think past setting "creative" questions which might win them accolades at assessment conferences but don't help struggling students much.

 

[kuruman]

One thing I used to tell my students is that about 50% of their score on a test depends on their frame of mind. A lot of them are scared of physics and their fear gets in the way of their performance. I reassure anyone who expresses such a fear that nothing "horrible" will happen to them during the test. Then I point out that, statistically, a higher percentage of the student population are injured or even die in car accidents than during physics tests, yet all students fearlessly and routinely get in cars and drive away without a moment's thought. I know I have hit the target when the response is something like "Oh, I never thought of it that way."

Part of the job is to allay these fears and build the self-confidence that students need to start believing that they can solve anything you might throw at their faces. They achieve that enhanced state of awareness by doing physics problems rather than by reading someone else's solution, That aligns very well with the PF Homework Helpers' principal principle not to give answers away.