Strength of Materials- Asymmetric, simply supported beam problem

[dorado29]

I'm working on a problem but I've hit a road block..

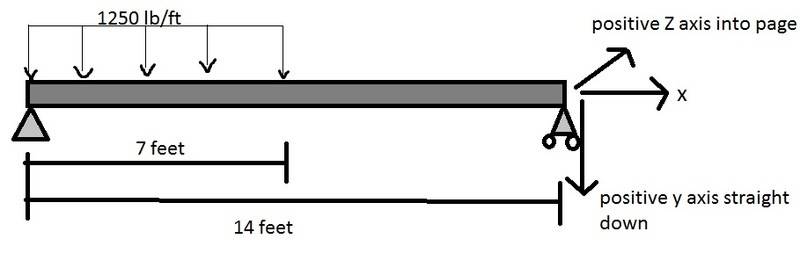
Then the cross section of the piece is here:

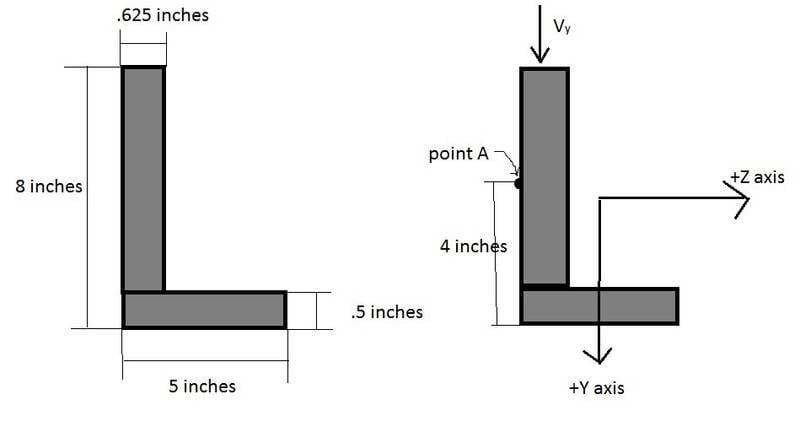
The first part of the problem is to determine Iy, Iz, and Iyz of the member.. I found the y value of the centroid to be 2.8587" and the z value of the centroid to be 1.0734" using the bottom left corner as the origin. From there I did the following:

Iz = 1/12(5)(.5)³ + 2.5(.25 - 2.8587)² + 1/12(.625)(7.5)³ + 4.6875(.3125 - 1.0734)²

and something similar for Iy and Iyz. All said and done I got

Iz = 48.112 in⁴
Iy = 13.163 in⁴
Iyz = -14.266 in⁴

Anywho, I then used that to get:

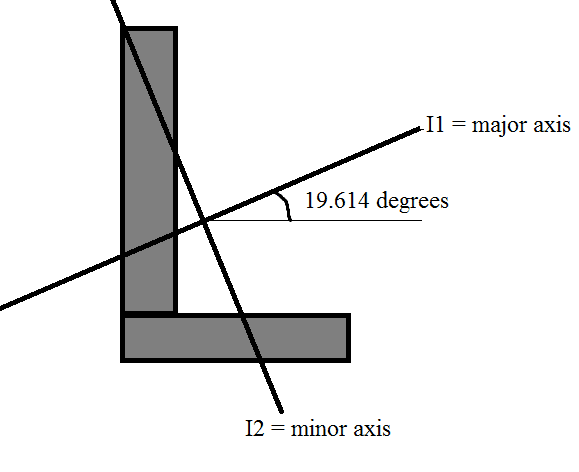
Where I1 = 53.196 in⁴
and I2 = 8.0788 in⁴

Radius of gyration:
Rmax = 2.7205 in
Rmin = 1.0602 in

~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~~

The next part of the problem is to find the max stress (be it tensile or compressive) at the far left hand side. I calculated the reaction force of the support to be 6562.5 lbf in the negative Y direction (the opposite of V_y in picture 2) and no moments at all which makes sense considering that the far left side is essentially "exposed" to air.

Am I correct to treat this like V_y is simply negative? Another part of me wants to say that the reaction force from the support is applied to the bottom of the member and I don't know if that changes anything or not..

It seems that the max stress will be solely from the shear stress caused by the support force? I'm trying to figure that out but my book only covered shear stress for symmetrical beams. I remember my professor saying something about using just the webbing for the shear analysis(?) Like treat it as if only the vertical, 8 inch high, .625 inch thick webbing was there then do a simple shear analysis on that piece.. Can somebody point me in the right direction please?

 

[SteamKing]

In order to analyze these beam problems properly, you should calculate the support reactions and construct the shear force and bending moment diagrams. The maximum bending moment will occur at a location where the shear force is zero. However, since you are looking to calculate the max. stress, there may be a location along the beam where the combined stress due to bending and shear may be a maximum. The magnitude of the max. stress can be determined using Mohr's circle. Analyzing an L-section is tricky because of the asymmetrical nature of the beam. The shear center for an L-section lies outside of the beam itself, and applying a shear force anywhere except thru the shear center leads to the creation of a torsional moment on the beam.