Stuck on the sides of a triangle problem

[tony700]

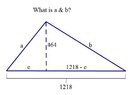
I have figured out the triangle's height and base, but I need to figure out sides a and b. I have tried Pythagorean theorem and similar triangle ratios, but it is not working out. Please help. See picture below. Thank you.View attachment 6489

 

[mathmari]

We have that two right triangles and from the Pythagorean Theorem for those two we get:
$$464^2+e^2=a^2$$ and $$464^2+(1218-e)^2=b^2$$

From the Geometric mean theorem we have that $$464^2=e\cdot (1218-e)$$

Now we have three unknown variables, $a,b,e$, and three equations. So, we can find the values for $a,b,e$.

 

[Greg]

Is the angle contained by $a$ and $b$ equal to $90^\circ$? For that matter, what is the complete problem?