Student sliding bag along floor in elevator

[member 731016]

Homework Statement

Pls see below

Relevant Equations

Pls see below

For this problem,

The solution is,

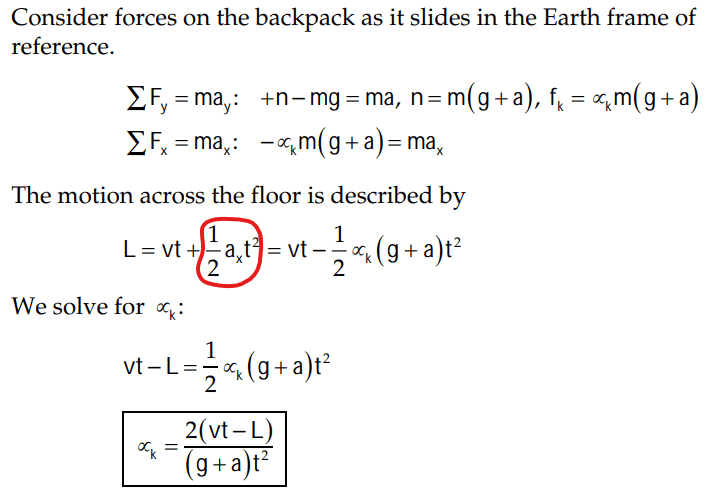
However, is the reason why they don't do $-0.5a_xt^2$ because the negative of the acceleration has already taken care of itself?

Many thanks!

 

[anuttarasammyak]

The answer seems to make
a_x=-\alpha_k (g+a)<0
negative. You can make it positve one with your setting of $-0.5a_xt^2$.

 

[member 731016]

The answer seems to make
a_x=-\alpha_k (g+a)<0
negative. You can make it positve one with your setting of $-0.5a_xt^2$.

Than you for your reply @anuttarasammyak !