mathmari
Gold Member
MHB
- 4,984
- 7
Hey! 
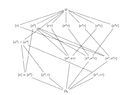
I want to make the diagram for the dihedral group $D_6$:
Subroups of order $2$ : $\langle \tau \rangle$, $\langle \sigma\tau\rangle$, $\langle\sigma^2\tau\rangle$, $\langle\sigma^3\tau\rangle$, $\langle\sigma^4\tau\rangle$, $\langle\sigma^5\tau\rangle$, $\langle\sigma^3\rangle$
Subgroups of order $3$ : $\langle\sigma^2\rangle$, $\langle\sigma^4\rangle$
Subgroups of order $6$ : $\langle \sigma \rangle$, $\langle \sigma^5\rangle$, $\langle\sigma^2, \tau\rangle$, $\langle\sigma^2, \sigma\tau\rangle$
Are there more for each order? (Wondering)
The subgroups of order $4$ are those that are isomorphic to $\mathbb{Z}_4$ or to $\mathbb{Z}_2\times\mathbb{Z}_2$, right? (Wondering)
There are no elements of order $4$, so there are no subgroups of order $\mathbb{Z}_4$, right? (Wondering)
Are the subgroups that are isomorphic to $\mathbb{Z}_2\times\mathbb{Z}_2$ the $\langle a,b\rangle$, for all $a, b$ the elemennt of order $2$
($a,b \in \{\tau, \sigma\tau, \sigma^2\tau , \sigma^3\tau , \sigma^4\tau, \sigma^5\tau , \sigma^3\}$ ) ? (Wondering)
I want to make the diagram for the dihedral group $D_6$:
Subroups of order $2$ : $\langle \tau \rangle$, $\langle \sigma\tau\rangle$, $\langle\sigma^2\tau\rangle$, $\langle\sigma^3\tau\rangle$, $\langle\sigma^4\tau\rangle$, $\langle\sigma^5\tau\rangle$, $\langle\sigma^3\rangle$
Subgroups of order $3$ : $\langle\sigma^2\rangle$, $\langle\sigma^4\rangle$
Subgroups of order $6$ : $\langle \sigma \rangle$, $\langle \sigma^5\rangle$, $\langle\sigma^2, \tau\rangle$, $\langle\sigma^2, \sigma\tau\rangle$
Are there more for each order? (Wondering)
The subgroups of order $4$ are those that are isomorphic to $\mathbb{Z}_4$ or to $\mathbb{Z}_2\times\mathbb{Z}_2$, right? (Wondering)
There are no elements of order $4$, so there are no subgroups of order $\mathbb{Z}_4$, right? (Wondering)
Are the subgroups that are isomorphic to $\mathbb{Z}_2\times\mathbb{Z}_2$ the $\langle a,b\rangle$, for all $a, b$ the elemennt of order $2$
($a,b \in \{\tau, \sigma\tau, \sigma^2\tau , \sigma^3\tau , \sigma^4\tau, \sigma^5\tau , \sigma^3\}$ ) ? (Wondering)