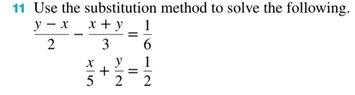MHB Substitution Method to solve linear simultaneous equation

AI Thread Summary
The discussion focuses on solving a system of linear equations using the substitution method. The user transformed the equations into a common denominator and derived two equations: 5y - 5x = 1 and 5y + 2x = 5. After substituting, they found x = 4/7, but expected the solution to be x = 0. A suggestion was made to multiply the first equation by 6 and simplify to potentially correct the solution. The conversation highlights the importance of careful manipulation of equations in the substitution method.
Yazan975
Messages
30
Reaction score
0
View attachment 8419

What I have done:

I changed all fractions to common denom and that gave me

5y-5x=1 (1) *I numbered the fractions
5y+2x=5 (2)

Then: 5y=5-2x

Substitute into equation 1
(5-2x)-5x=1
5-7x=1
x=4/7

Thing is my answer says I should be getting x=0

Any hints?
 

Attachments

  • Screen Shot 2018-09-18 at 5.48.11 PM-min.png
    Screen Shot 2018-09-18 at 5.48.11 PM-min.png
    10.6 KB · Views: 118
Mathematics news on Phys.org
When you multiply the first equation by $6$ and simplify, you should get $y-5x=1$.
 

Thread 'Trigonometry problem of interest'

Seemingly by some mathematical coincidence, a hexagon of sides 2,2,7,7, 11, and 11 can be inscribed in a circle of radius 7. The other day I saw a math problem on line, which they said came from a Polish Olympiad, where you compute the length x of the 3rd side which is the same as the radius, so that the sides of length 2,x, and 11 are inscribed on the arc of a semi-circle. The law of cosines applied twice gives the answer for x of exactly 7, but the arithmetic is so complex that the...
View full post »

Thread 'Six Pencil Puzzle'

Is it possible to arrange six pencils such that each one touches the other five? If so, how? This is an adaption of a Martin Gardner puzzle only I changed it from cigarettes to pencils and left out the clues because PF folks don’t need clues. From the book “My Best Mathematical and Logic Puzzles”. Dover, 1994.
View full post »
Thread 'Imaginary Pythagoras'

Thread 'Imaginary Pythagoras'

I posted this in the Lame Math thread, but it's got me thinking. Is there any validity to this? Or is it really just a mathematical trick? Naively, I see that i2 + plus 12 does equal zero2. But does this have a meaning? I know one can treat the imaginary number line as just another axis like the reals, but does that mean this does represent a triangle in the complex plane with a hypotenuse of length zero? Ibix offered a rendering of the diagram using what I assume is matrix* notation...
View full post »

Similar threads

MHB Number patterns and sequences - Tn Term
Replies
1
Views
2K
B How can I properly distribute fractions when solving a set of linear equations?
Replies
7
Views
2K
B Need assistance with an unusual quadratic solution method
Replies
4
Views
1K
MHB Solving Equivalent Expressions Using Subtraction Method
Replies
6
Views
2K
Solve these simultaneous equations that involve vectors
Replies
6
Views
2K
MHB Evaluating Chosen Numbers in Quadratic Inequality
Replies
7
Views
2K
Solve for x and y in the given algebra problem involving fractions
Replies
25
Views
3K
MHB What is the Common Core method for solving 2x + 3x?
Replies
2
Views
2K
MHB Show that the solution is not suitable....
Replies
10
Views
3K
MHB Fixed point,, Jacobi- & Newton Method, Linear Systems
Replies
7
Views
2K

Hot Threads

Recent Insights

Back
Top