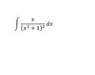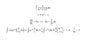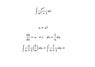- #1
You are using an out of date browser. It may not display this or other websites correctly.
You should upgrade or use an alternative browser.
You should upgrade or use an alternative browser.
Substitution Rule in Indefinite Integrals
- Thread starter phillyolly
- Start date
In summary, the substitution rule in differentiation is the reverse of the chain rule. This technique can be applied to a problem to get a different solution.
Physics news on Phys.org
- #2
phillyolly
- 157
- 0
Actually, one second. I am solving it right now. Will post a solution.
- #3
Mark44
Mentor
- 37,780
- 10,169
Substitution is the reverse of the chain rule in differentiation. For example,
[tex]\frac{d}{dx}(x^3 - 2)^4~=~4(x^3 - 2)^3~3x^2[/tex]
The corresponding indefinite integral is
[tex]\int 12x^2(x^3 - 2)^3~dx[/tex]
Here, we let u = x3 - 2, so du = 3x2~dx, so
[tex]\int 12x^2(x^3 - 2)^3~dx~=~\int 4*3x^2~(x^3 - 2)^3~dx~=~\int 4 u^3 du~=~\frac{4u^4}{4} + C~=~(x^3 - 2)^4 + C[/tex]
Can you see how this technique (it's not a rule) could be applied to your problem?
[tex]\frac{d}{dx}(x^3 - 2)^4~=~4(x^3 - 2)^3~3x^2[/tex]
The corresponding indefinite integral is
[tex]\int 12x^2(x^3 - 2)^3~dx[/tex]
Here, we let u = x3 - 2, so du = 3x2~dx, so
[tex]\int 12x^2(x^3 - 2)^3~dx~=~\int 4*3x^2~(x^3 - 2)^3~dx~=~\int 4 u^3 du~=~\frac{4u^4}{4} + C~=~(x^3 - 2)^4 + C[/tex]
Can you see how this technique (it's not a rule) could be applied to your problem?
- #4
- #5
Mark44
Mentor
- 37,780
- 10,169
Correct as far as it goes. You still need to undo your substitution.
Also, u = x2 + 1 ==> du = 2xdx. You have x and dx, so you can get the 2 that's needed by multiplying by 2 and then multiplying on the outside of the integral by 1/2. That way, you're really multiplying by 1, which doesn't change the value of the integrand.
Also, u = x2 + 1 ==> du = 2xdx. You have x and dx, so you can get the 2 that's needed by multiplying by 2 and then multiplying on the outside of the integral by 1/2. That way, you're really multiplying by 1, which doesn't change the value of the integrand.
- #6
- #7
- #8
Mark44
Mentor
- 37,780
- 10,169
Sure, that works.
Another substitution that isn't so obvious is to let u = sec2t (using t for theta). Then du = 2sec(2t)tan(2t)dt
[tex]\int sec(2t)tan(2t)dt = \frac{1}{2}\int 2sec(2t)tan(2t)dt = \frac{1}{2}\int du= \frac{u}{2} + C = \frac{sec(2t)}{2} + C[/tex]
Another substitution that isn't so obvious is to let u = sec2t (using t for theta). Then du = 2sec(2t)tan(2t)dt
[tex]\int sec(2t)tan(2t)dt = \frac{1}{2}\int 2sec(2t)tan(2t)dt = \frac{1}{2}\int du= \frac{u}{2} + C = \frac{sec(2t)}{2} + C[/tex]
- #9
- #10
phillyolly
- 157
- 0
Mark44 said:Sure, that works.
Another substitution that isn't so obvious is to let u = sec2t (using t for theta). Then du = 2sec(2t)tan(2t)dt
[tex]\int sec(2t)tan(2t)dt = \frac{1}{2}\int 2sec(2t)tan(2t)dt = \frac{1}{2}\int du= \frac{u}{2} + C = \frac{sec(2t)}{2} + C[/tex]
OH! This one is much prettier than mine!
- #11
Mark44
Mentor
- 37,780
- 10,169
This will work, but will require another substitution.phillyolly said:Thank you very much!
I am also stuck on this one. ex has been always tricky for me.
Here's a different approach: u = ex + 1, du = exdx
[tex]\int \frac{e^x~dx}{e^x + 1}=\int \frac{du}{u}= ln(u) + C = ln(e^x+ 1) + C[/tex]
Since u = ex + 1 > 0 for all real x, I didn't need to include absolute values on the argument to the natural log function.
- #12
phillyolly
- 157
- 0
Thank you a lot, Mark44!
FAQ: Substitution Rule in Indefinite Integrals
What is the substitution rule in indefinite integrals?
The substitution rule, also known as the u-substitution method, is a technique used in solving indefinite integrals. It involves substituting a part of the integrand with a new variable, usually denoted as u, in order to simplify the integral.
When should I use the substitution rule in indefinite integrals?
The substitution rule should be used when the integrand contains a function within a function, or when the integrand involves a complicated expression that can be simplified by substitution.
How do I perform the substitution rule in indefinite integrals?
To perform the substitution rule, follow these steps:1. Identify the function within the function or the complicated expression in the integrand.2. Substitute it with a new variable, usually denoted as u.3. Rewrite the integral in terms of u.4. Replace all occurrences of the original function or expression with u.5. Solve the new integral in terms of u.6. Substitute back u with the original function or expression.
What are the benefits of using the substitution rule in indefinite integrals?
The substitution rule allows for the simplification of complicated integrands, making it easier to evaluate the integral. It also helps in finding antiderivatives of functions involving nested functions.
Are there any limitations to the substitution rule in indefinite integrals?
Yes, the substitution rule may not work for all integrals. In some cases, the substitution may lead to a more complicated integral, making it difficult to solve. It is important to carefully choose the substitution variable to avoid this issue.
Similar threads
- Replies
- 3
- Views
- 2K
- Replies
- 4
- Views
- 1K
- Replies
- 4
- Views
- 2K
- Replies
- 22
- Views
- 2K
- Replies
- 1
- Views
- 728
- Replies
- 11
- Views
- 2K
- Replies
- 2
- Views
- 907
- Replies
- 2
- Views
- 1K
- Replies
- 12
- Views
- 3K
- Replies
- 5
- Views
- 794
Share: