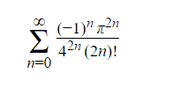Umar
- 36
- 0
Hey guys! I just have a question regarding finding the sum of an infinite series. Attached is the image of the question. I've tried to use the ratio test but it doesn't give me the result I need which happens to be 1/sqrt(2). I feel like this is one of those power series questions, but I'm not quite sure how to deal with this. If anyone could help out, that would be greatly appreciated!
View attachment 6430
View attachment 6430