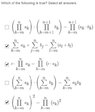- #1
- 51
- 0
As per the image, I am supposed to select all the valid statements. Apparently I'm only partially correct, and so I took another look at the statements.
I believe the third statement is wrong, since \(\displaystyle c * (a_m*a_{m+1}*a_{m+2}*...*a_n)\) =/= \(\displaystyle (c*a_m)(c*a_{m+1})(c*a_{m+2})*...*(c*a_n)\)
Thus there should only be two answers. Am I correct on this?
I believe the third statement is wrong, since \(\displaystyle c * (a_m*a_{m+1}*a_{m+2}*...*a_n)\) =/= \(\displaystyle (c*a_m)(c*a_{m+1})(c*a_{m+2})*...*(c*a_n)\)
Thus there should only be two answers. Am I correct on this?
