Sun Shade Projection type of problem

[unknown101]

Homework Statement

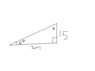
Two math students erect a sun shade on the beach. The shade is 1.5 m tall, 2 m wide, and makes an angle of 60° with the ground. What is the area of shade that the students have to sit in at 12 noon (that is, what is the projection of the shade onto the ground)? (Assume the sun’s rays are shining directly down)

Homework Equations

I've attached the formula

The Attempt at a Solution

I tried drawing a diagram with 2m at the bottom and the height being 1.5. I know I'm supposed to use the projection formula. After that I'm lost.

 

[LowlyPion]

It's just a simple triangle isn't it?

The width is going to be the same. (The direction || to the ground.)

Since the shade is determined by the vertical rays, and they give you the length of the hypotenuse, ... and the angle ... looks like you are just a trig function choice away from an answer.

 

[unknown101]

I don't think they give you the length of the hypotenuse. I drew a right angle triangle with 2m at the bottom and the length of the side with the 90 degree angle is 1.5. The angle at the bottom left is 60 degrees. what hypotenuse are you talking about?

 

[LowlyPion]

I don't think they give you the length of the hypotenuse. I drew a right angle triangle with 2m at the bottom and the length of the side with the 90 degree angle is 1.5. The angle at the bottom left is 60 degrees. what hypotenuse are you talking about?

Take a sheet of paper. And hold it an angle to your desk. Your paper has a length and width. It's projection then is what function of θ relative to your desk?

Regardless of which way you hold your paper, one of the dimensions will be || to the desk and the other at angle θ.

Simply apply some trig function of θ to the area, and you have it.

So ... which trig function?

 

[unknown101]

Would 1.5m be the length or 2m. I think 2m would be the length of the hypotenuse because it is always the longest side. But how do you know for sure. Would I use the sin ratio the find the length after?

 

[LowlyPion]

Would 1.5m be the length or 2m. I think 2m would be the length of the hypotenuse because it is always the longest side. But how do you know for sure. Would I use the sin ratio the find the length after?

It doesn't matter which really. It all goes into the product that is the area.

As to your function it depends on how you are taking θ.

 

[unknown101]

I'm totally lost I don't know what I would do after. I made a diagram but i don't know where to go from there.

 

[unknown101]

I might have a solution can someone tell me if its correct.

sin60degrees=opp/hyp
sin60=x/15
x=1.5(sin60)
= 1.5(0.866)
x= 1.299m

Therefore the the area that students will have to sit will be 1.299m^2

 

[LowlyPion]

I might have a solution can some tell me if its correct.

sin60degrees=opp/hyp
sin60=x/15
x=1.5(sin60)
= 1.5(0.866)
x= 1.299m

Therefore the the area that students will have to sit will be 1.299m^2

It's area. You need to multiply by the 2m to get your m²

Then you should have the answer.

 

[unknown101]

So the final answer is 2.598m^2?

 

[LowlyPion]

So the final answer is 2.598m^2?

Double check your angle.

The sun is coming straight down.

The 60 degrees is with the ground.

So wouldn't that be cos 60 degrees along the ground?

 

[unknown101]

Double check your angle.

The sun is coming straight down.

The 60 degrees is with the ground.

So wouldn't that be cos 60 degrees along the ground?

So then it should be cosx=adj/hyp
=2/1.5
=1.33


cos60=x/15
=1.5 X cos60
x=1.5 X 0.5
x=1.5 X 0.5
x=0.75
x= 0.75 X 2m
x= 1.5m^2

Why would it be this instead of the sin which I used before.

 

[LowlyPion]

I can't see your drawing.

It is my reading of the problem that the shed makes an angle of 60 degrees with the ground. Then in that configuration, with the roof angled up, I think it is Cos 60, as the ground is the adjacent side to the angle.

So isn't then the area projected to the ground cos60*A, where A = area at angle = 0?

If there is a drawing, that is different than this, please explain.

 

[unknown101]

Basically my drawing is a right angle triangle with 1.5m being the hypotenuse and 2m being the adjacent side. 60 degrees is between the measurements. The post that I posted before is it right?

 

[LowlyPion]

Basically my drawing is a right angle triangle with 1.5m being the hypotenuse and 2m being the adjacent side. 60 degrees is between the measurements. The post that I posted before is it right?

Isn't the roof 2m x 1.5m?

Doesn't this rectangular piece then make an angle with the ground at 60 degrees?

 

[unknown101]

Yes it does. So is my solution correct?

 

[LowlyPion]

Yes it does. So is my solution correct?

Not if it involves taking sin60 of the area.

If the roof is at the angle 60 with the ground, then the ground (where the shadow is) would be the adjacent side to the 60 degree angle.

 

[unknown101]

So then it should be cosx=adj/hyp
=2/1.5
=1.33


cos60=x/15
=1.5 X cos60
x=1.5 X 0.5
x=1.5 X 0.5
x=0.75
x= 0.75 X 2m
x= 1.5m^2

Why would it be this instead of the sin which I used before.

I redid the problem after you said I might be wrong. So is the right way to do it?

 

[LowlyPion]

I redid the problem after you said I might be wrong. So is the right way to do it?

Yes. That's the right answer.

Area = 1.5 * 2 = 3 m²

Projected area = cos60 * Area = 3 * .5 = 1.5

 

[unknown101]

Thanks a lot for your help