MHB Supeerstar's questions at Yahoo Answers regarding optimizing quadratic functions

[MarkFL]

Here are the questions:

Help with solving these quadratic worded problems?


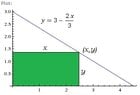
1) A rectangle is constructed so that one vertex is at the origin, and another vertex is on the graph of y=3 - 2x/3 where x >0 and y>0 and adjacent sides are on the axes. what is the maximum possible area of the rectangle?

2) What is the minimum value of 3x^2 +7x -2 if -3 ≤ x ≤ 0 ?

3) What is the maximum value of 3x^2 + 7x - 2 if 0 ≤ x ≤ 3?

I have posted a link there to this topic so the OP can see my work.

 

[MarkFL]

Hello supeerstar,

1.) Let's look at a plot of the given line and a rectangle constructed as instructed:

View attachment 1525

We see the area of the rectangle is:

$$

We also see that we require $$.

Since $$ we may write:

$$

Observing this is a parabola opening downwards, we know the maximum must occur on the axis of symmetry, given by:

$$

And so we find:

$$

And so the maximum area of the rectangle is 3 square units.

For problems 2.) and 3.), let:

$$

We find the axis of symmetry for the given quadratic is:

$$

Since this is a quadratic opening upwards, we know the global minimum is:

$$

For any interval wholly to the right of the axis of symmetry, we know the maximum value of the function is at the right end-point. Hence:

2.) $$

3.) $$