- #1
genxium
- 141
- 2
I've just watch MIT open course 8.03, vibrations and waves, lecture 14, and think of a weird problem,
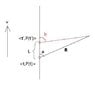
if a particle(with charge) in vacuum, say a proton or an electron, regardless of the size because of far-field consideration, like what's shown in the attachment, is moving along a straight line with a constant velocity [itex]v,[/itex]
assume the current time is [itex]t,[/itex] current position of the particle is [itex]P(t),[/itex] and a view point which is very far away from the particle's current position, so that the EM wave emitted at [itex]<t,P(t)>[/itex] has to travel for a non-ignorable time [itex]\triangle t[/itex] to reach my view point, and say the time when this EM wave reaches my view point will be [itex]T.[/itex]
Could anyone tell me, if there exist 1 or more points on the straight line, say [itex]P(t'),[/itex] that the EM wave emitted at [itex]<t',P(t')>[/itex] will also reach my view point at [itex]T.[/itex]
P.S. From my calculation, a point [itex]P(t')[/itex] satisfies that [itex]|P(t')-P(t)|=\frac{2 \cdot vR \cdot (c-v \cdot cos a)}{c^2-v^2},[/itex] by cosine law, the reason I don't trust this result is obvious:
From my calculation , there's only 1 such point that matches the requirement, but think of it recursively, if 1 such point is found, we can always find a new one based on the previous one with arguments [itex]<t,P(t), R, a>,[/itex] then the series have to be infinite.
if a particle(with charge) in vacuum, say a proton or an electron, regardless of the size because of far-field consideration, like what's shown in the attachment, is moving along a straight line with a constant velocity [itex]v,[/itex]
assume the current time is [itex]t,[/itex] current position of the particle is [itex]P(t),[/itex] and a view point which is very far away from the particle's current position, so that the EM wave emitted at [itex]<t,P(t)>[/itex] has to travel for a non-ignorable time [itex]\triangle t[/itex] to reach my view point, and say the time when this EM wave reaches my view point will be [itex]T.[/itex]
Could anyone tell me, if there exist 1 or more points on the straight line, say [itex]P(t'),[/itex] that the EM wave emitted at [itex]<t',P(t')>[/itex] will also reach my view point at [itex]T.[/itex]
P.S. From my calculation, a point [itex]P(t')[/itex] satisfies that [itex]|P(t')-P(t)|=\frac{2 \cdot vR \cdot (c-v \cdot cos a)}{c^2-v^2},[/itex] by cosine law, the reason I don't trust this result is obvious:
From my calculation , there's only 1 such point that matches the requirement, but think of it recursively, if 1 such point is found, we can always find a new one based on the previous one with arguments [itex]<t,P(t), R, a>,[/itex] then the series have to be infinite.