The Tortoise-Man
- 95
- 5
I have a question about natural limitations when the superposition principle for circuits is applicable. Possibly there is a quite elementary reason why the problem I'm going to present next fails, but up to now I haven't a precise reason why that's exactly the case. Could somebody help?
Consider the following situation which rather confuses me:
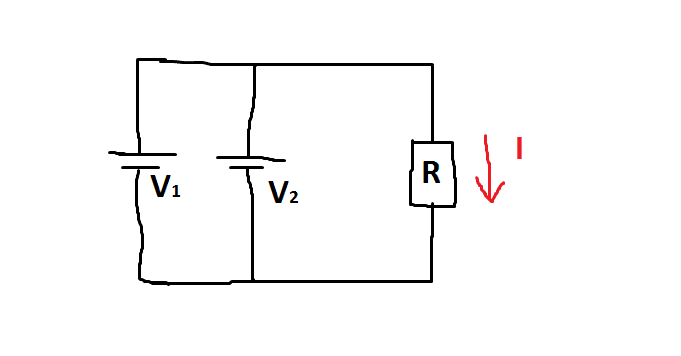
The voltage sources ##S_1## and ##S_2## with voltages ##V_1## and ##V_2## which we assume to be equal: ##V_1= V_2 (=V)##
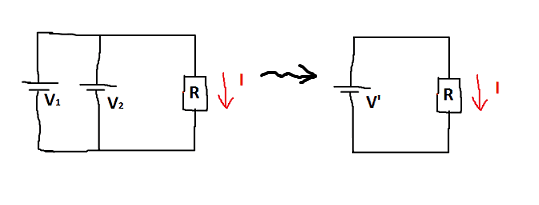
We want to calculate the current ##I## across the resistor ##R## using two methods: 1) usual standard way we learn to add up two parallel voltages and 2) aplication of superposition prinicple.For 1): Due to basic calucation rules for two parallel voltage sources with SAME voltage ##V_1= V_2 ## we can make a replacement:
Now if we set ##I_1## to be the current in
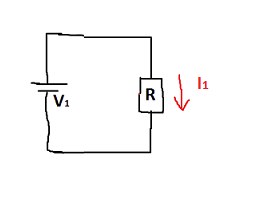 then ## I= 2I_1##.
then ## I= 2I_1##.
For 2): On the other hand if we try to apply the superposition principle to this circuit and short out say ##S_2## then we
obtain
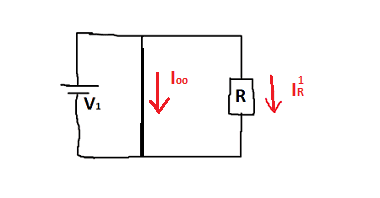 with ##I_{\infty}= \infty ## and ##I^1_R=0## since we have shorted ##S_2##. From symmetrical
with ##I_{\infty}= \infty ## and ##I^1_R=0## since we have shorted ##S_2##. From symmetrical
reasons in the same game shorting out ##S_1## we obtain ##I^2_R=0## and therefore ##I= I^1_R + I^2_R =0## and that
contradicts to the considerations above.
So seemingly in this situation the superposition principle fails because 2) make no sense at experience level. But on the other hand I read that the only obstruction to use superposition principle is the requirement that the circuit/network should be linear, that's all as far I know.
This one is linear. But seemingly the application of superposition here gives absurd results.
Where is the error in my reasonings?
Consider the following situation which rather confuses me:
The voltage sources ##S_1## and ##S_2## with voltages ##V_1## and ##V_2## which we assume to be equal: ##V_1= V_2 (=V)##
We want to calculate the current ##I## across the resistor ##R## using two methods: 1) usual standard way we learn to add up two parallel voltages and 2) aplication of superposition prinicple.For 1): Due to basic calucation rules for two parallel voltage sources with SAME voltage ##V_1= V_2 ## we can make a replacement:
Now if we set ##I_1## to be the current in
For 2): On the other hand if we try to apply the superposition principle to this circuit and short out say ##S_2## then we
obtain
reasons in the same game shorting out ##S_1## we obtain ##I^2_R=0## and therefore ##I= I^1_R + I^2_R =0## and that
contradicts to the considerations above.
So seemingly in this situation the superposition principle fails because 2) make no sense at experience level. But on the other hand I read that the only obstruction to use superposition principle is the requirement that the circuit/network should be linear, that's all as far I know.
This one is linear. But seemingly the application of superposition here gives absurd results.
Where is the error in my reasonings?