Superposition Problem- Circuits

  • Context: Engineering 
  • Thread starter Thread starter RoKr93
  • Start date Start date
  • Tags Tags
    Circuits Superposition
Click For Summary

Discussion Overview

The discussion revolves around a circuit analysis problem involving superposition to find the output voltage coefficients in relation to multiple independent sources. Participants are addressing the application of circuit laws and methods such as voltage division and current division to derive the output voltage and power delivered to a resistor.

Discussion Character

  • Homework-related
  • Mathematical reasoning
  • Technical explanation
  • Debate/contested

Main Points Raised

  • One participant proposes using voltage division to find the first coefficient, suggesting vout1 = 0.2Vs1.
  • Another participant expresses uncertainty about the second coefficient for Is2, stating vout2 = 20Is2.
  • A participant describes the challenge of calculating vout3 when Is3 is the only source active, noting the need to consider the circuit configuration with R1, R2, and R3.
  • One participant suggests using current division to find the current i2 and subsequently vout3, providing a formula for vout3 based on Is3 and the resistances.
  • There is a concern raised about the total output voltage exceeding the expected value when substituting values into the derived equations, indicating a potential error in calculations.
  • A later reply prompts checking the work related to the coefficient for Is2, suggesting possible inaccuracies in earlier calculations.

Areas of Agreement / Disagreement

Participants express varying levels of confidence in their calculations, with some uncertainty regarding the coefficients and the total output voltage. There is no consensus on the correctness of the derived values or the approach to finding vout3.

Contextual Notes

Participants have not fully resolved the calculations for the coefficients, and there are indications of missing assumptions or potential errors in the application of circuit laws. The discussion reflects ongoing refinement of ideas rather than established conclusions.

Who May Find This Useful

This discussion may be useful for students or individuals studying circuit analysis, particularly those interested in superposition and the application of circuit laws in problem-solving contexts.

RoKr93
Messages
21
Reaction score
0

Homework Statement


2013-06-19193003_zpsc110ea7a.jpg


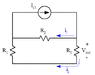
For the above circuit, find the coefficients of the linear relationship vout = a1vs1 + a2is2 + a3is3 by superposition. Then find the power delivered to R3 when vs1 = 100 V, is2 = 2 A, and is3 = 4 A. Given: R1 = 20 Ω, R2 = 60 Ω, and R3 = 20 Ω.


Homework Equations



Ohm's Law: V = IR

KVL: V1 + V2 + ... Vn = 0 for closed loops

KCL: I1 + I2 + ... In = 0 going in an out of a node

Voltage Division: V1 = Vsource * (R1/(R1+R2))


The Attempt at a Solution


I think I got the first two coefficients (though I could be incorrect). I found vout1 = vs1*(R3/(R1+R2+R3)) = 0.2Vs1 through voltage division. I'm pretty certain that's correct.

I also found that vout2 = Is2*R3 = 20Is2, though I'm not quite as certain about that.

But I absolutely cannot wrap my head around finding vout3 (when all independent sources are eliminated except Is3). I understand that in that situation, the Is2 branch essentially disappears and we are left with Is3 in parallel with a branch with R2 and a branch with R1 and R3, but we can't combine those since vout3 must stay isolated. I'm not sure what to do.
 
Physics news on Phys.org
You have a classic current divider scenario with current Is3 being divided between two branches. You know the total resistance of each of the branches.

attachment.php?attachmentid=59714&stc=1&d=1371688705.gif


Alternatively, consider converting Is3 and R2 to their Thevenin equivalent and finding the resulting current and then the potential across R3.
 

Attachments

  • Fig1.gif
    Fig1.gif
    2 KB · Views: 545
So I want to use current division to find i2, then multiply that by R3 to get my voltage value?

i2 = Is3*(R2/(R1+R2+R3))
vout3 = i2R3
vout3 = Is3*((R2*R3)/(R1+R2+R3))

After substituting values in, vout3 comes out to be 12. Unfortunately either that or one of my previous solutions is wrong- a later part of the problem states that the total vout must be 100 V when vs1 = 100 V, is2 = 2 A, and is3 = 4 A. And (0.2*100) + (20*2) + (12*4) is 108. Did I go about finding vout3 the wrong way?
 
Check your work for the coefficient for Is2.
 

Similar threads

Engineering Is My Understanding of the Current Amplification Circuit Correct?
  • · Replies 12 ·
Replies
12
Views
2K
Engineering Why is a differential amplifier considered the same as a subtractor?
  • · Replies 1 ·
Replies
1
Views
2K
Engineering Is my method of solving this correct? Superposition theorem
  • · Replies 15 ·
Replies
15
Views
3K
Engineering Calculating the voltage at a certain Resistor
  • · Replies 3 ·
Replies
3
Views
2K
Engineering Solve Superposition Theorem for R1, R2 Circuit
  • · Replies 18 ·
Replies
18
Views
3K
Engineering Why is the output voltage of the subtractor calculated like this?
  • · Replies 5 ·
Replies
5
Views
2K
Engineering AC Circuit Phasors: Find I1, I2, I3
  • · Replies 26 ·
Replies
26
Views
3K
Calculating the voltage in an OP-amp circuit with a current source
  • · Replies 1 ·
Replies
1
Views
2K
Engineering Find the unknown resistance in this series circuit
  • · Replies 7 ·
Replies
7
Views
4K
Comp Sci Need help finding the resistor size for a circuit (Ohm's law)
  • · Replies 1 ·
Replies
1
Views
2K