Supremum Property (AoC) .... etc .... Another question/Issue

[Math Amateur]

I am reading Houshang H. Sohrab's book: "Basic Real Analysis" (Second Edition).

I am focused on Chapter 2: Sequences and Series of Real Numbers ... ...

I need help with another issue/problem with Theorem 2.1.45 concerning the Supremum Property (AoC), the Archimedean Property, and the Nested Intervals Theorem ... ...

Theorem 2.1.45 reads as follows:

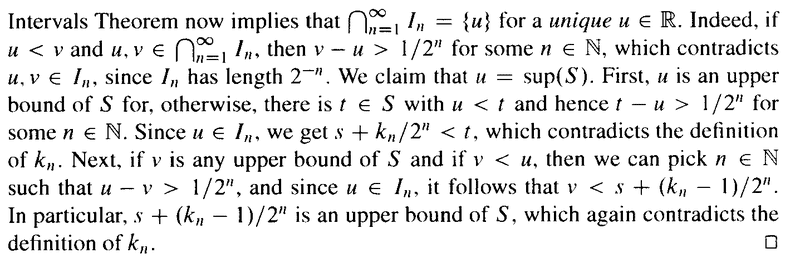In the above proof by Sohrab, we read the following:

" ... ... Thus while (by definition) $s + \frac{k_n}{2^n} = s + \frac{2 k_n}{ 2^{n + 1} }$ is an upper bound of $S, s + \frac{ 2 k_n - 2 }{ 2^{n + 1} } = s + \frac{k_n - 1 }{2^n}$ is not. Therefore, either $k_{ n+1 } = 2k_n$ or $k_{ n+1 } = 2k - 1$ and $I_{ n + 1 } \subset I_n$ follow. ... ... "I am uncertain and somewhat confused by the logic of the above ...

I am not sure of the argument that either $k_{ n+1 } = 2k_n$ or $k_{ n+1 } = 2k - 1$ ... can someone please explain in simple terms why it is valid ... ..

I am also not sure exactly why $I_{ n + 1 } \subset I_n$ ... if anything it seems to me that $I_{ n + 1 } = I_n$ ... again, can someone please explain in simple terms why $I_{ n + 1 } \subset I_n$ ... that is that $I_{ n + 1 }$ is a proper subset of $I_n$ ... ...

[ ***EDIT*** Just checked and found that Sohrab is using \subset in the sense which includes equality ... so using $\subset$ as meaning $\subseteq$ ... ]Help will be appreciated ...

Peter
==========================================================================================The above theorem concerns the Supremum Property, the Archimedean Property and the Nested Intervals Theorem ... so to give readers the context and notation regarding the above post I am posting the basic information on these properties/theorems ...

 

[andrewkirk]

In the above proof by Sohrab, we read the following:

" ... ... Thus while (by definition) $s + \frac{k_n}{2^n} = s + \frac{2 k_n}{ 2^{n + 1} }$ is an upper bound of $S, s + \frac{ 2 k_n - 2 }{ 2^{n + 1} } = s + \frac{k_n - 1 }{2^n}$ is not. Therefore, either $k_{ n+1 } = 2k_n$ or $k_{ n+1 } = 2k - 1$ and $I_{ n + 1 } \subset I_n$ follow. ... ... "I am uncertain and somewhat confused by the logic of the above ...

I am not sure of the argument that either $k_{ n+1 } = 2k_n$ or $k_{ n+1 } = 2k - 1$ ... can someone please explain in simple terms why it is valid ... ..

I am also not sure exactly why $I_{ n + 1 } \subset I_n$ ... if anything it seems to me that $I_{ n + 1 } = I_n$ ... again, can someone please explain in simple terms why $I_{ n + 1 } \subset I_n$ ... that is that $I_{ n + 1 }$ is a proper subset of $I_n$

I assume you accept the statement that $s + \frac{ 2 k_n - 2 }{ 2^{n + 1} }$ is not an upper bound of $S$. If not, this post won't help.

$k_{n+1}$ is defined as the smallest $m\in\mathbb N$ such that $s+k_{n+1}/2^{n+1}$ is an UB for $S$. We know that $s+(2k_n-2)/2^{n+1}$ is not an UB, therefore it must be too small to be an UB. So we must have $k_{n+1}> 2k_n-2$.

How much bigger does $k_{n+1}$ have to be? We know that $2k_n$ is big enough. So $k_{n+1}\leq 2k_n$.

The only integers $m$ that satisfy $2k_n-2 < m \leq 2k_n$ are those two the text names.

 

[Math Amateur]

Thanks Andrew ... now understand ...

Your post was most helpful ...

Peter