Petrus
- 702
- 0
Calculate the area of the surface of rotation which occurs when the curve
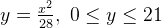 rotate in y-axe.
rotate in y-axe.
I start with $$x=\sqrt{28y}$$ then $$f'(x)=\frac{14}{\sqrt{28y}}$$
so we got
$$2\pi\int_0^{21}\sqrt{28y}\sqrt{1+(\frac{14}{\sqrt{28y}})}^2$$
then I rewrite as $$\int_0^2\sqrt{28y}\sqrt{1+\frac{196}{28y}}$$
$$\sqrt{28y}\sqrt{1+\frac{196}{28y}}<=>\sqrt{28y+196}$$
So I got $$2\pi\int_0^{21}\sqrt{28y+196}$$ and if Integrate it I get
$$\frac{(28y+196)^{1.5}}{1.5*28}$$ Is this correct?
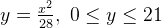
I start with $$x=\sqrt{28y}$$ then $$f'(x)=\frac{14}{\sqrt{28y}}$$
so we got
$$2\pi\int_0^{21}\sqrt{28y}\sqrt{1+(\frac{14}{\sqrt{28y}})}^2$$
then I rewrite as $$\int_0^2\sqrt{28y}\sqrt{1+\frac{196}{28y}}$$
$$\sqrt{28y}\sqrt{1+\frac{196}{28y}}<=>\sqrt{28y+196}$$
So I got $$2\pi\int_0^{21}\sqrt{28y+196}$$ and if Integrate it I get
$$\frac{(28y+196)^{1.5}}{1.5*28}$$ Is this correct?