- #1
destroyer130
- 18
- 0
Thanks for checking this out. Here's the problem:

I attempted to do it by using parametrize it into spherical coordinate.
r(r,t) = (x= cost, y= sint, z=r)
dS=|r[itex]_{u}[/itex] x r[itex]_{v}[/itex]| dA = r[itex]\sqrt{2}[/itex] dA
dA = rdrdt
[itex]\int\int[/itex]x[itex]^{2}[/itex]z[itex]^{2}[/itex]dS = [itex]\int\int[/itex][itex]\sqrt{2}[/itex] cos[itex]^{2}[/itex] r[itex]^{6}[/itex] drdt
I check my solution manual and this is how they do it. My integral has r[itex]^{6}[/itex] factor. However, solution's only has r[itex]^{5}[/itex] instead. I am very confused because these two are supposed to be from the same source...
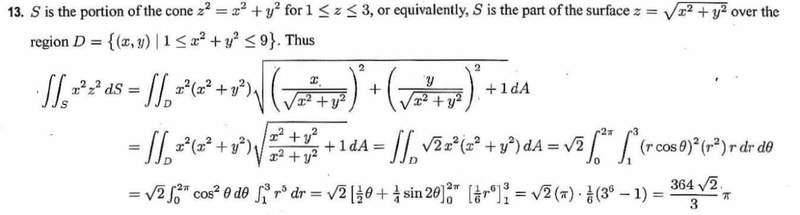
I attempted to do it by using parametrize it into spherical coordinate.
r(r,t) = (x= cost, y= sint, z=r)
dS=|r[itex]_{u}[/itex] x r[itex]_{v}[/itex]| dA = r[itex]\sqrt{2}[/itex] dA
dA = rdrdt
[itex]\int\int[/itex]x[itex]^{2}[/itex]z[itex]^{2}[/itex]dS = [itex]\int\int[/itex][itex]\sqrt{2}[/itex] cos[itex]^{2}[/itex] r[itex]^{6}[/itex] drdt
I check my solution manual and this is how they do it. My integral has r[itex]^{6}[/itex] factor. However, solution's only has r[itex]^{5}[/itex] instead. I am very confused because these two are supposed to be from the same source...