evinda
Gold Member
MHB
- 3,741
- 0
Hello! :D
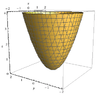
Find the surface that is created by the intersection of the paraboloid $x^2+y^2-z=0$ and the plane $z=2$.
Is the intesection: $x^2+y^2=2,z=2$? Or is it not the asked surface?(Thinking)
Find the surface that is created by the intersection of the paraboloid $x^2+y^2-z=0$ and the plane $z=2$.
Is the intesection: $x^2+y^2=2,z=2$? Or is it not the asked surface?(Thinking)