lukegxhycj
- 8
- 0
- Homework Statement
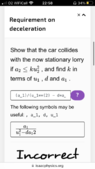
- A lorry travelling along a narrow road with speed u1
applies its brakes to give a uniform deceleration of magnitude a1
. At the same time a car, a distance d behind the lorry and travelling in the same direction with speed u2
, applies its brakes to give a uniform deceleration of a2
Part A
Show that the car collides with the now stationary lorry if a2≤ku2^2
, and find k in terms of u1 , d and a1
- Relevant Equations
- All SUVAT equations
s1=-u1^2/2a1
s2=-u2^2/2a2
s2>s1+d
(If distance the car stops is bigger than the distance the lorry stops plus the initial distance then they will crash)
(sub s1 and s2 in)
-u2^2/2a2 > -u1^2/2a1+d
Switch 2a2 with whole left side of equation.
-u2^2/(-u1^2/2a1)+d > 2a2
Make the (d)a fraction by multiplying denominator and numerator by 2a1
-u2^2*(2a1/-u1^2+2a1d) > 2a2
Cancel the minus time minus on the left side.
u2^2*(a1/u1^2+2a1d)>a2
K=a1/u1^2+2a1d
And it was wrong apparently
s2=-u2^2/2a2
s2>s1+d
(If distance the car stops is bigger than the distance the lorry stops plus the initial distance then they will crash)
(sub s1 and s2 in)
-u2^2/2a2 > -u1^2/2a1+d
Switch 2a2 with whole left side of equation.
-u2^2/(-u1^2/2a1)+d > 2a2
Make the (d)a fraction by multiplying denominator and numerator by 2a1
-u2^2*(2a1/-u1^2+2a1d) > 2a2
Cancel the minus time minus on the left side.
u2^2*(a1/u1^2+2a1d)>a2
K=a1/u1^2+2a1d
And it was wrong apparently
Attachments
Last edited:



 ##\qquad## !
##\qquad## !