brotherbobby
- 750
- 169
- Homework Statement
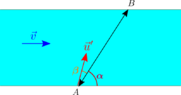
- A man swims across a river from ##A## to ##B## and back from ##B## to ##A##, following the line ##AB## as shown in the figure below. The distance between the two points is ##S##. The velocity of the river is ##v## and is the same over the entire width of the river, staying constant. As shown in the figure, the line ##AB## makes an angle ##\alpha## with the direction of the river flow and the man swims with a velocity ##u'## at an angle ##\beta## to the line ##AB## for both occasions. ##\\[10pt]##.
Calculate the time taken by the man for his to and fro journey.##\\[10pt]##
- Relevant Equations
- 1. The relative velocity ##\vec{v}_M=\vec u\;\text{(say)}## of the man with respect to the earth is the vector sum of his velocity with respect to the river ##\vec{v}_{MR} = \vec u'\; \text{(in this problem)}\;## and the velocity of the river relative to earth ##\vec {v}_R = \vec v\;\text{(in this problem)}\;##. Thus ##\vec u = \vec u' + \vec v####\\[10pt]##
2. In order for the man to swim in the given direction ##AB## (see figure below), it is necessary that the components of his velocity and that of the river ##\textbf{normal}## to the line ##AB## cancel out. Thus ##u' \sin\beta = v \sin\alpha##. ##\\[10pt]##
Attempt : It is clear at the outset that, since the velocity of river is constant, the man will not take the same time for the forward and reverse journeys. For both journeys however, the Relevant Equation 2 above will have to hold, since he is constrained to move along ##AB##: ##
\begin{equation}
u' \sin\beta = v \sin\alpha
\end{equation}
##
##\\[10 pt]##
The distance ##AB## is equal to ##S##. Hence the time for the forward journey is given by
##
\begin{equation*}
t_1 = \frac{S}{u'\cos\beta+v \cos\alpha}
\end{equation*}
##
(2) Backward motion : The motion back to ##A## looks like that on the left. The velocity of the man in the direction ##B\rightarrow A## is given by ##u_2 = u' \cos\beta - v\cos\alpha##. ##\\##
The distance ##BA## is equal to ##S##. Hence the time for the backward journey is given by
##
\begin{equation*}
t_2 = \frac{S}{u'\cos\beta-v \cos\alpha}
\end{equation*}
##The total time for these motions ##t= t_1+t_2 = \frac{S}{u'\cos\beta+v \cos\alpha} + \frac{S}{u'\cos\beta-v \cos\alpha} = \frac{2u'\cos\beta}{u'^2\cos^2\beta - v^2\cos^2\alpha}S##. ##\\[10pt]##
Let me put the final answer for the total time with a better look : $$\boxed{t = \frac{2u'\cos\beta}{u'^2\cos^2\beta - v^2\cos^2\alpha}S} \checkmark$$
This is the answer given in the book, so I am right. However, it ignores the fact that perpendicular to the motion ##A\rightarrow B\;\text{or}\; B\rightarrow A##, the velocity of the swimmer and the river cancel (refer equation 1 above).
That equation said ##u' \sin\beta = v \sin\alpha \Rightarrow u'^2 \sin^2\beta = v^2 \sin^2\alpha\Rightarrow u'^2-u'^2 \cos^2\beta = v^2-v^2 \cos^2\alpha \Rightarrow u'^2 \cos^2\beta - v^2 \cos^2\alpha = u'^2-v^2##.##\\[10pt]##
Thus the time of travel is $$\boxed{t = \frac{2u\cos\beta}{u'^2-v^2}S}$$Doubt : Assuming I am right, the above answer in blue raises a tricky question.
The angle of the path relative to river flow, ##\alpha## is absent!
It means therefore that the man will take the same time along any path he chooses provided he keeps the distance ##S## fixed. This can be managed by him not going all the way to the other bank but stopping somewhere in between before returning.
But intuitively, does this make sense? Clearly, the time of travel for the onward journey, ##t_1## would be less with decreasing angle ##\alpha##. This is because while the component of his velocity along the path of travel remains the same (##u'\cos\beta##), the contribution from the river (##v\cos\alpha##) increases with decreasing ##\alpha##. My conclusion is that it also means when he returns, his velocity will be smaller due to an increase in (negative) ##v\cos\alpha## and the increase and decrease will compensate.
Am I correct in resolving my doubt? A hint would be welcome.