- #1
Gregg
- 459
- 0
This is a question about the swinging Atwood machine. I have completed the first half of the problems which involved finding a lagrangian involving the obvious co-ordinates, finding the conjugate momenta and writing a new Hamiltonian:
[tex] H = E = \frac{p_{\theta}^2}{2mr^2}+\frac{p_r^2}{2(m+M)}-gr(m \cos \theta - M) [/tex]
We are then given the expression for the energy under the following transformations:
[tex] r = \frac{\xi^2 +\eta^2}{2} [/tex]
[tex] \theta = 2\arctan\left(\frac{\xi^2-\eta^2}{2\xi\eta}\right) [/tex]
Which is:
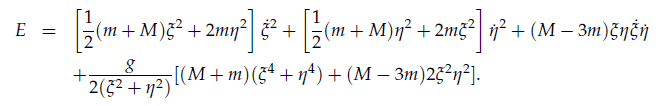
We are looking at the case where M=3m (the system is integrable) Rather than just changing a sign somewhere in E I decided to use
[tex] L=2T-E [/tex]
After plugging this in and doing some cancellations I found that:
[tex] T = 2m(\xi^2\eta^2)(\dot{\eta}^2+\dot{\xi}^2) [/tex]
[tex] L=2m(\eta^2+\xi^2)(\dot{\eta}^2+\dot{\xi}^2)-2mg \frac{\xi^4+\eta^4}{\xi^2+\eta^2} [/tex]
Now I have the Lagrangian I can find the canonically conjugate momenta for xi and eta as the partial derivatives of my Lagrangian with respect to their corresponding time derivatives. Plugging this into the equation for the Hamiltonian I get a new H:
[tex] H = \frac{p_{\eta}^2+p_{\xi}^2}{8m(\eta^2+\xi^2)}+2mg \frac{\eta^4+\xi^4}{\eta^2+\xi^2} [/tex]
Then we come to the bit I am stuck on the part about the Hamilton-Jacobi equation. I don't know if I've made a mistake somewhere but I thought the transformations were supposed to simplify the problem?
Using HJE
[tex] \frac{1}{8m(\xi^2+\eta^2)} \left[ \left( \frac{\partial S}{\partial \xi} \right)^2 + \left( \frac{\partial S}{\partial \eta} \right)^2 \right] + 2mg \frac{\eta^4 + \xi^4 }{\eta^2+\xi^2} + \frac{\partial S}{\partial t} = 0 [/tex]
So they're separable so take S,
[tex] S(\eta, \xi, t) = W_1(\xi) +W_2(\eta) - Et [/tex]
where E is the energy.
Then I deduce that:
[tex] \frac{1}{8m(\xi^2+\eta^2)}\left[ \left( \frac{d W_1(\xi)}{d \xi} \right)^2 + \left( \frac{d W_2(\eta)}{d \eta} \right)^2 \right] + 2mg \frac{\eta^4 + \xi^4 }{\eta^2+\xi^2} = E [/tex]
Then because it's separable or at least we are assuming it is:
[tex] \left( \frac{d W_1(\xi)}{d \xi} \right)^2 = 8\xi^2m (E-2mg \xi^2) [/tex]
[tex] \left( \frac{d W_2(\eta)}{d \eta} \right)^2 = 8\eta^2m (E-2mg \eta^2) [/tex]
Which is solvable giving:
[tex] W_1(\xi) = -\frac{\sqrt{2} (E-2m\eta^2)^{3/2}}{2\sqrt{m}} [/tex]
[tex] W_2(\eta) = -\frac{\sqrt{2} (E-2m\xi^2)^{3/2}}{2\sqrt{m}} [/tex]
Am I wrong in splitting it up this way? The question says to separate them with separation constant I

What is separation constant I, and have I separated properly? Is the Hamiltonian correct? I am unsure on how going from here I will eventually get an EoM. And what the point of the transformations were really.
[tex] H = E = \frac{p_{\theta}^2}{2mr^2}+\frac{p_r^2}{2(m+M)}-gr(m \cos \theta - M) [/tex]
We are then given the expression for the energy under the following transformations:
[tex] r = \frac{\xi^2 +\eta^2}{2} [/tex]
[tex] \theta = 2\arctan\left(\frac{\xi^2-\eta^2}{2\xi\eta}\right) [/tex]
Which is:
We are looking at the case where M=3m (the system is integrable) Rather than just changing a sign somewhere in E I decided to use
[tex] L=2T-E [/tex]
After plugging this in and doing some cancellations I found that:
[tex] T = 2m(\xi^2\eta^2)(\dot{\eta}^2+\dot{\xi}^2) [/tex]
[tex] L=2m(\eta^2+\xi^2)(\dot{\eta}^2+\dot{\xi}^2)-2mg \frac{\xi^4+\eta^4}{\xi^2+\eta^2} [/tex]
Now I have the Lagrangian I can find the canonically conjugate momenta for xi and eta as the partial derivatives of my Lagrangian with respect to their corresponding time derivatives. Plugging this into the equation for the Hamiltonian I get a new H:
[tex] H = \frac{p_{\eta}^2+p_{\xi}^2}{8m(\eta^2+\xi^2)}+2mg \frac{\eta^4+\xi^4}{\eta^2+\xi^2} [/tex]
Then we come to the bit I am stuck on the part about the Hamilton-Jacobi equation. I don't know if I've made a mistake somewhere but I thought the transformations were supposed to simplify the problem?
Using HJE
[tex] \frac{1}{8m(\xi^2+\eta^2)} \left[ \left( \frac{\partial S}{\partial \xi} \right)^2 + \left( \frac{\partial S}{\partial \eta} \right)^2 \right] + 2mg \frac{\eta^4 + \xi^4 }{\eta^2+\xi^2} + \frac{\partial S}{\partial t} = 0 [/tex]
So they're separable so take S,
[tex] S(\eta, \xi, t) = W_1(\xi) +W_2(\eta) - Et [/tex]
where E is the energy.
Then I deduce that:
[tex] \frac{1}{8m(\xi^2+\eta^2)}\left[ \left( \frac{d W_1(\xi)}{d \xi} \right)^2 + \left( \frac{d W_2(\eta)}{d \eta} \right)^2 \right] + 2mg \frac{\eta^4 + \xi^4 }{\eta^2+\xi^2} = E [/tex]
Then because it's separable or at least we are assuming it is:
[tex] \left( \frac{d W_1(\xi)}{d \xi} \right)^2 = 8\xi^2m (E-2mg \xi^2) [/tex]
[tex] \left( \frac{d W_2(\eta)}{d \eta} \right)^2 = 8\eta^2m (E-2mg \eta^2) [/tex]
Which is solvable giving:
[tex] W_1(\xi) = -\frac{\sqrt{2} (E-2m\eta^2)^{3/2}}{2\sqrt{m}} [/tex]
[tex] W_2(\eta) = -\frac{\sqrt{2} (E-2m\xi^2)^{3/2}}{2\sqrt{m}} [/tex]
Am I wrong in splitting it up this way? The question says to separate them with separation constant I
What is separation constant I, and have I separated properly? Is the Hamiltonian correct? I am unsure on how going from here I will eventually get an EoM. And what the point of the transformations were really.