Switching reference frames between two intersecting lines

[John3509]

Homework Statement

Daisy and her boyfriend Alf decide to have a bicycle race. Because the rates at which Daisy and Alf can ride are 720 and 660 meters per minutes respectfully Alf is given a head start of 2 minutes.

Relevant Equations

y=mx+b

I got no problem with the arithmetic and solving it, finding the intersection of 2 lines is nothing, but I decided to play around with the problem and explore it more and ran into a strange problem, why can't I shift the X axis up? Let me explain.

The problem can be set up from 2 different perspectives.

We start counting time from Daisy's perspective and hey line goes through the origin, so that when her timer starts Alf is already his speed * 2 minutes ahead.

This is what I mean (1st image)

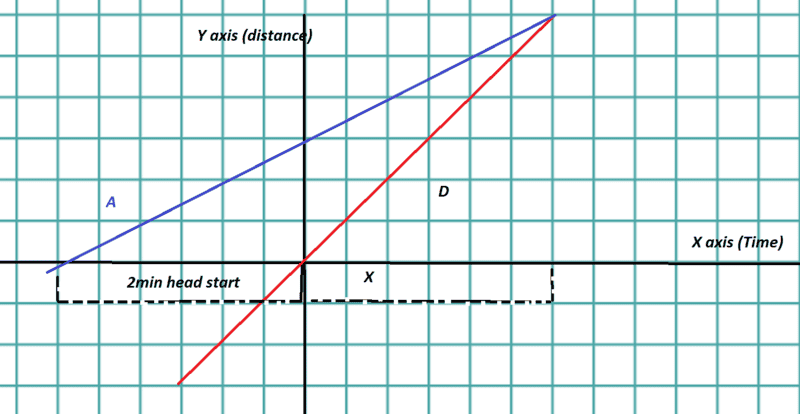The corresponding equations are:

distance(daisy) = 720x

distance(albert) = 660x + 660(2)

the algebra here is straight forwards, the x here will be the time it takes for her to overtake (intersect)

x=22
But we can also view from Alfs perspective, the timer starts when he is at origin, meaning Daisy at T=0 is 2 times her speed behind in terms of distance, and she will reach Y=0 at 2 minutes.

Here is an image for this, (2nd one)

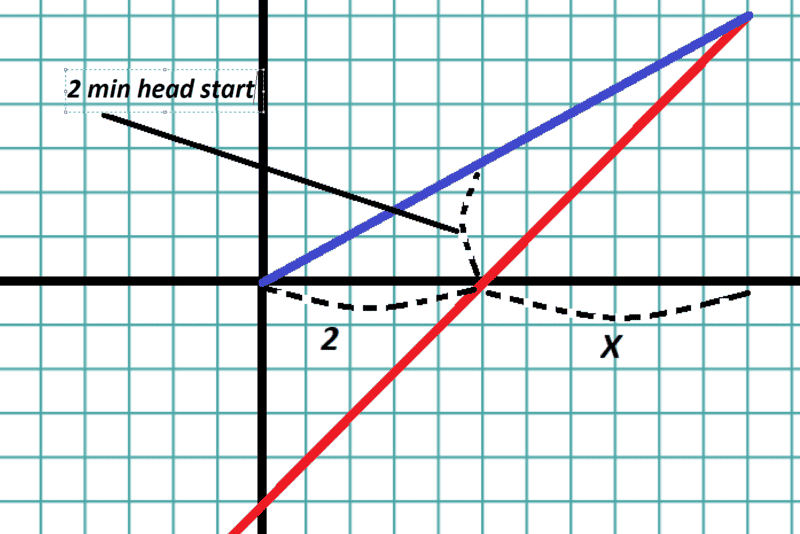The corresponding equation for this perspective are:

d = 720x - 720(2)

a = 660x

the difference here is this x is the time it takes for Daisy to catch up +2 of head start time

indeed the result here is 24
But wait, if we draw another line here, (3rd image)

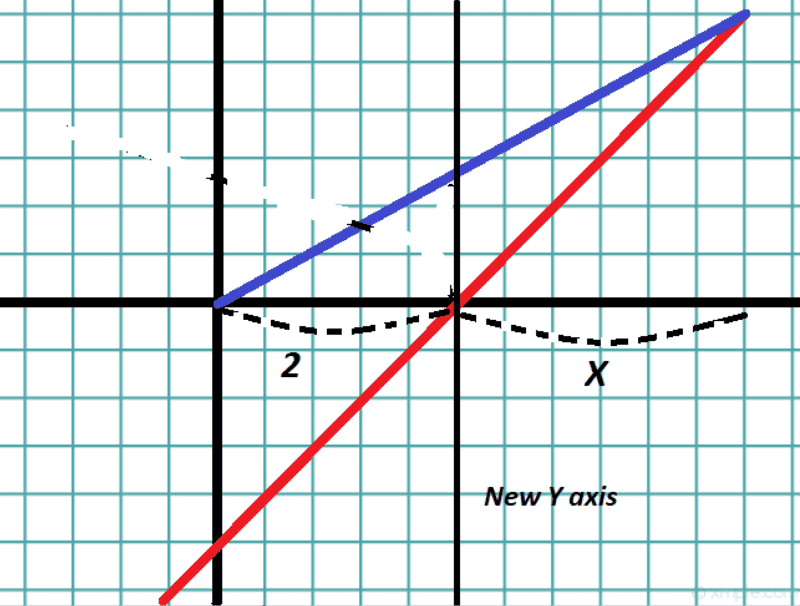
we essentially have the same perspective as before.

We can switch perspective by creating a new Y axis, lets call it Z

where Z=X-2

Plugging this into these formulas we get

d= 720 (z+2) - 720(2)

d= 720z

and

a = 660(z+2)

a= 660z + 660(2)

Indeed these are the same relationships as in my original set up (1st picture)

But now here is my problem.

Lets go back to my first set up, (1st image)

where Daisy is at the origin

and now instead I want to shift the X axis up, to get Alf it the origin.

Like this, (4rth picture)

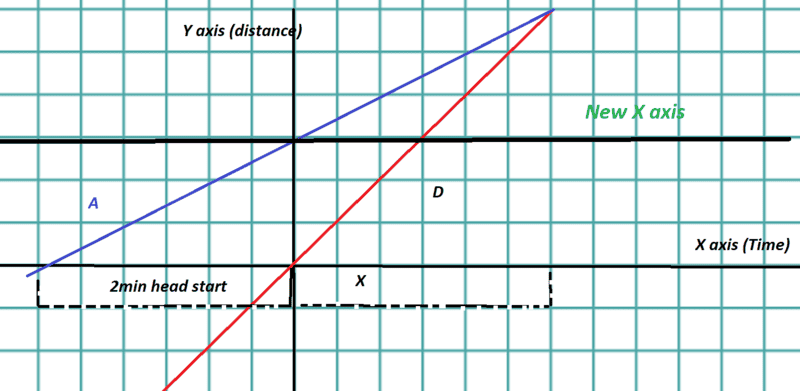
looks alot like the second set up, with Daisy going into the negatives a T=0

so what is the formula for the switch?

Lets call this new X axis W

Y = W + 660(2)

plugging it in to the first scenario

W(daisy) = 720x - 660(2)

W(Alf) = 660x

Ok, we got something similar to the second set up now, except the Hight for Diasy is wrong.

Why?

And how would I switch by shifting the X axis up?

 

[hmmm27]

I got no problem with the arithmetic and solving it, finding the intersection of 2 lines is nothing

Since your graphs clearly show that Daisy's velocity is twice that of Alf, and she suddenly appears - in motion - after Alf's been moving for 1 minute (not 2 as claimed in the problem statement), I would humbly suggest that you do indeed got problems with the arithmetic.

Also, who is Albert ?

Strongly suggested is to clearly do the math and graph for the original problem first. Pick whether you want to have the "start" of the race be at t=0 or t=-2, and show the time Daisy is just sitting on her bike enjoying a sports drink. Also, races usually have a "finish" parameter.

 

[John3509]

Since your graphs show that the Daisy's velocity is twice that of Alf, and she appears, moving after Alf's been moving for 1 minute (not 2 as claimed in the problem statement)

The graphs are not to scale, just meant to show in general the concept.

Im assuming you are referring to the first graph since I posted 4 of them? And the graph shows that at T=0 alf is 2(660) meters ahed, as claimed in the problem statement. They are just lines, they can go on forever, im sure you could figure that out but if you really want to be pedantic about it maybe daisy was board and decided to bike to the starting line?

I would humbly suggest that you indeed do got problems with the arithmetic.

what? what "problems"? I asked why shifting the y axis works but shifting the x does not.

Could you clearly do the math, and the graph, first. Strongly suggested is to show Daisy's movement (or lack of same) throughout, and to choose whether you want your time axis to start at 0 or -2.

I already did that. You do realize I already solved the problem, right? x is 22 . And switching where I start the time axis is literally the point of this exercise, but you tell me to choose one, if you don't want to help me with what Im asking that's fine but why reply then

 

[hmmm27]

but why reply then

From the title, I thought the post was about changing - rather than translating - reference frames (ie: going from an external observer's POV, to Daisy or Alf's), which looked mildly interesting.

Okay, so this pair has $t=0$ at Alf's start :

$d_A=660t$​

$d_D=720(t-2)$​

Following that we can translate to one where $t=0$ when Daisy starts :

$d_A=660(t+2)$​

$d_D=720t$​

And, from there we can go to a pair that has Alf at $d=0$ when Daisy starts (at $t=0$) :

$d_A=660t$​

$d_D=720t-1320$​

Looks good to me ; seems to match your answer.

 

[hmmm27]

Ok, we got something similar to the second set up now, except the Hight for Diasy is wrong.

What does that even mean, and why do you consider it to be wrong. Does Fla's Hight look wrong to you, as well ? How about Albert's Dwith ?

 

[hmmm27]

Okay, so having been very nicely Told to be less of a dick...

Highly suggested (again) is to draw a proper graph, for the first example :

Pick appropriate scaling for each axis, such that the plots fit nicely (and evenly) onto the graph.​

​

Hints:​

• the parameters are nice, round numbers that scale easily ; no need to explicitly label the gridlines, except where necessary.
• since all the "action" is taking place in one quadrant, there's no reason to show the other three ; ie: (0,0) doesn't need to be centered on the page.

Plotting should be from the time Alf starts his run until Daisy crashes into Alf. Daisy's plot needs to include time spent chewing gum.​

Note: whatever the original book-problem was probably included an explicit or implicit "finish line" (since it's a race), which is immaterial to your purposes.​

​

When that's done, since your math already works, translating the axes graphically should be pretty intuitive, and will probably solve whatever issue you have - which you haven't made clear, yet - which got you here in the first place.

 

[John3509]

From the title, I thought the post was about changing - rather than translating - reference frames (ie: going from an external observer's POV, to Daisy or Alf's)

I wasn't aware there is a difference between translating and changing reference frames, what is the difference?

It took me like 45 minutes to make those graphs in paint with my mouse. I dont see the utility in making a to scale graphs when these are sufficient to to demonstrate the concept at play here, they intersect in the 1st quadrant and from one perspective one goes through the origin and the other has a positive y intercept and from another the other one goes though the origin and the other has a negative y intercept, you can visualize switching between the two as the axis being moved.

Also its not needed since you got the same equations that I got it seems I didn't do anything wrong, It's just a matter of understanding the math now.

will probably solve whatever issue you have - which you haven't made clear, yet - which got you here in the first place.

My issue was why I can move the Y axis back and forth and solve the problem correctly but I cant move the x axis?

When we move the x axis up we are going back to a point of view where alf is at the origin and daisy is at a negative y intercept, but now the y intercept is different. If I try to solve it now my setting them equal to each other I would get the wrong answer.

Looking at the 4th graph, I can see that the 2 minute head start bracket is 6 units on the graph and in the new x axis that 2 minutes is only 3 units on the graph, I can see it scales down since its a triangle, but the translation should take care of all that. But it doesn't, so how would I do it?

 

[John3509]

Oh I got it, 1320/60 is 22 as well, I saw the different y intercepts and panicked I forgot in this reference frame there is no +2.

Anyway, whats the difference between translating and changing reference frames?

 

[hmmm27]

Right, so you're good, now ?

I wouldn't take my terminology as gospel, it was just what was closest at hand.

But, at a meta level, while the math for what you've been doing clearly involves moving a triangle around in Cartesian coordinates, your rhetoric has consistently been that of the triangle staying in the same spot, moving axes around. Different frames of reference.

But, I consider what we've been doing as "simply" translation, ie: moving something from point A to point B without changing its orientation. Still uses the same coordinate system.

Meanwhile, what I thought the thread was going to be about was something like plotting a graph from Daisy or Alf's point of view, rather than the external reference frame which I guess would be the road they're bicycling on.

 

[John3509]

Right, so you're good, now ?

I wouldn't take my terminology as gospel, it was just what was closest at hand.

But, at a meta level, while the math for what you've been doing clearly involves moving a triangle around in Cartesian coordinates, your rhetoric has consistently been that of the triangle staying in the same spot, moving axes around. Different frames of reference.

But, I consider what we've been doing as "simply" translation, ie: moving something from point A to point B without changing its orientation. Still uses the same coordinate system.

Meanwhile, what I thought the thread was going to be about was something like plotting a graph from Daisy or Alf's point of view, rather than the external reference frame which I guess would be the road they're bicycling on.

Yea im good, thanks. I always thought that's one and the same, all motion is relative after all. I don't understand half of what you said, but I guess that's because I'm not there yet.

what I thought the thread was going to be about was something like plotting a graph from Daisy or Alf's point of view,

So like alf staying in place and the starting line moving back. Interesting, I dont even know how to begin the math for something like that.

 

[hmmm27]

Math's the same : take Alf : in the original (the starting line pov), we're charting the difference between the starting line and Alf's movement :

start line : y=0 (x axis)
Alf : y = 660x

From Alf's point of view...
Alf : y=0 (x axis)
start line : y = -660x