Symmetry and two electron wave function

In summary, the conversation discusses the left-right symmetry of a system with two identical orbitals and the notation used to indicate the number of spin-up electrons in each orbital. The question is whether the left-right symmetry of the system requires the eigenstates of the Hamiltonian to be in a specific form, such as a superposition of left-right symmetric and anti-symmetric states. The response is that there is no strict requirement for the eigenstates to follow this symmetry, but it may be necessary for certain operators, such as the Hamiltonian. However, for a general state, there is no such requirement.
  • #1
hokhani
506
8
TL;DR Summary
Understanding the relation between system symmetry and wave-function symmetry
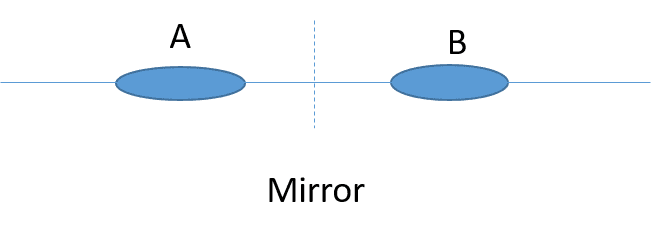
In the picture below we have two identical orbitals A and B and the system has left-right symmetry. I use the notation ##|n_{A \uparrow}, n_{A \downarrow},n_{B \uparrow},n_{B \downarrow}>## which for example ##n_{A \uparrow}## indicates the number of spin-up electrons in the orbital A. I would like to know is it possible to have an eigenstate as ##|1,1,0,0>## in this left-right symmetric system or, because of the symmetry of system, we must only have symmetric wave-functions as ##\frac{|1,1,0,0>\pm|0,0,1,1>}{\sqrt(2)}##?
Any help is appreciated.
Picture3.png
 
Physics news on Phys.org
  • #2
The only symmetry that states must follow is the one related to interchange of two identical particles.

(That said, if you need states to be eigenstates of some operators, like the Hamiltonian, then certain symmetries may need to be respected. But for a general state, there is no such requirement.)
 
  • Like
Likes Lord Jestocost and hokhani
  • #3
Thanks very much. In the second quantized form, the interchange of particles are included in the commutation of fermionic operators.
However, I would like to know whether the left-right symmetry of this system demands the eigenstates of the Hamiltonian be in the form ## \frac{1}{\sqrt(2)}(|1,1,0,0>\pm|0,0,1,1>)## or they can also have the form like ##|1,1,0,0>##?
 
  • #4
What is the Hamiltonian?
 
  • #5
I don't mean a specific Hamiltonian. I mean each left-right symmetric Hamiltonian for this system.
 
  • #6
Sorry if I didn't convey myself. To explain in a better way; for a left-right symmetric system, can we have the eigenstates which doesn't have this symmetry?
 
  • #7
hokhani said:
Sorry if I didn't convey myself. To explain in a better way; for a left-right symmetric system, can we have the eigenstates which doesn't have this symmetry?
If you have a degenerated eigenvalue with a left-right symmetric and a left-right anti-symmetric eigenstate, then take a superposition of them to get an eigenstate which is not left-right symmetric.
 
  • Like
Likes DrClaude and hokhani
  • #8
gentzen said:
If you have a degenerated eigenvalue with a left-right symmetric and a left-right anti-symmetric eigenstate, then take a superposition of them to get an eigenstate which is not left-right symmetric.
Thanks, I got it. Like the parity in one-particle system, provided that there is no degeneracy, the eigenstates must have even or odd symmetry as ##\frac{1}{\sqrt(2)}(|1,1,0,0>\pm|0,0,1,1>)##. Otherwise, there is no demand for symmetry of the eigenstates.
 

FAQ: Symmetry and two electron wave function

What is the significance of symmetry in the two-electron wave function?

Symmetry in the two-electron wave function is crucial because it determines the overall behavior and properties of the system. According to the Pauli exclusion principle, the wave function for two electrons must be antisymmetric with respect to the exchange of the two electrons. This antisymmetry ensures that no two electrons can occupy the same quantum state simultaneously, which is a fundamental principle in quantum mechanics.

How does the Pauli exclusion principle relate to the symmetry of the two-electron wave function?

The Pauli exclusion principle states that no two electrons can have the same set of quantum numbers in an atom. This principle is mathematically represented by the requirement that the two-electron wave function be antisymmetric under the exchange of the two electrons. If the spatial part of the wave function is symmetric, the spin part must be antisymmetric, and vice versa, ensuring the overall antisymmetry of the wave function.

What are the different types of symmetry that can be observed in the two-electron wave function?

The two-electron wave function can exhibit different types of symmetry based on the spatial and spin components. The spatial part of the wave function can be symmetric or antisymmetric, and the spin part can be in a singlet state (antisymmetric) or a triplet state (symmetric). The combination of these symmetries must result in an overall antisymmetric wave function to comply with the Pauli exclusion principle.

How does the symmetry of the two-electron wave function affect the energy levels of a system?

The symmetry of the two-electron wave function affects the energy levels because it determines the allowable states that the electrons can occupy. Symmetric and antisymmetric spatial wave functions correspond to different energy states. For example, in the hydrogen molecule, the symmetric spatial wave function corresponds to the bonding state with lower energy, while the antisymmetric spatial wave function corresponds to the antibonding state with higher energy.

What role does the exchange interaction play in the context of the two-electron wave function symmetry?

The exchange interaction arises due to the requirement of antisymmetry in the two-electron wave function and has significant implications for the energy and properties of electron pairs. It leads to an effective interaction between the electrons that depends on their relative spin orientation. In systems like the hydrogen molecule, the exchange interaction results in a lower energy for the singlet state (with antiparallel spins) compared to the triplet state (with parallel spins), influencing the overall stability and magnetic properties of the system.

Similar threads

I The Hamiltonian elements in Anderson dimer
Replies
4
Views
852
A Simultanious eigenstate of Hubbard Hamiltonian and Spin operator in tw
Replies
2
Views
1K
I Representation of Spin 1/2 quantum state
2
Replies
61
Views
4K
I Z2 symmetry in the hydrogen molecule when mapping to qubits
Replies
1
Views
1K
I The left-right symmetry and forbidden triplet spin state
Replies
21
Views
2K
I Measurement of an entangled Particles in two Different Bases
Replies
1
Views
897
I Measuring Entangled Particles in two different Basis
Replies
8
Views
1K
Partition function of modified Ising model
Replies
1
Views
1K
A Treatment of singlets in the Hubbard model
Replies
1
Views
1K
I Material Waves and Wave Functions
Replies
9
Views
1K

Hot Threads

Recent Insights

Back
Top