System of two pulleys and three masses

[Tlurk]

Homework Statement

I have a system with two pulleys and three masses where we have two outer masses on each end of the connecting rope and one middle mass at the centre of the rope. The length of the rope, the space between the pulleys and the pulley size are chosen arbitrarily. At first, all masses are equal, but we're supposed to change the middle mass later.
a) Can the system be at rest?
b) If so, what is the position of the three masses?
c) What happens if we change the middle mass?

Relevant Equations

Newton's laws.
ΣF = 0
Basic trigonometry.

I used m₁=m₂=15,0kg
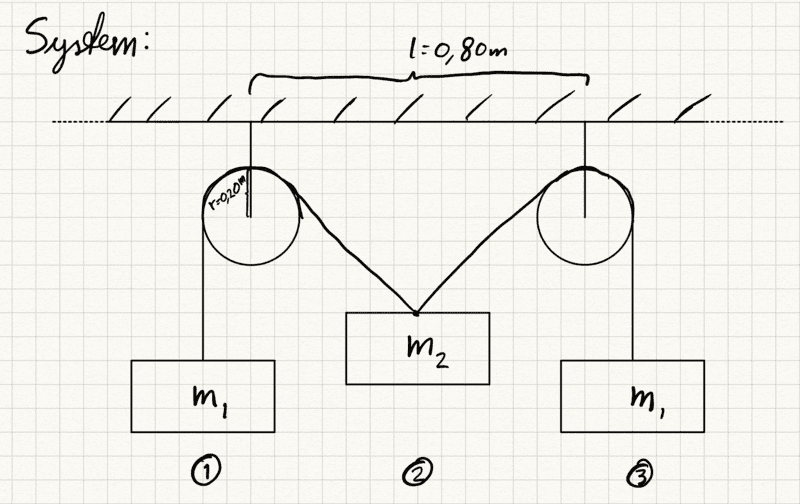
System:

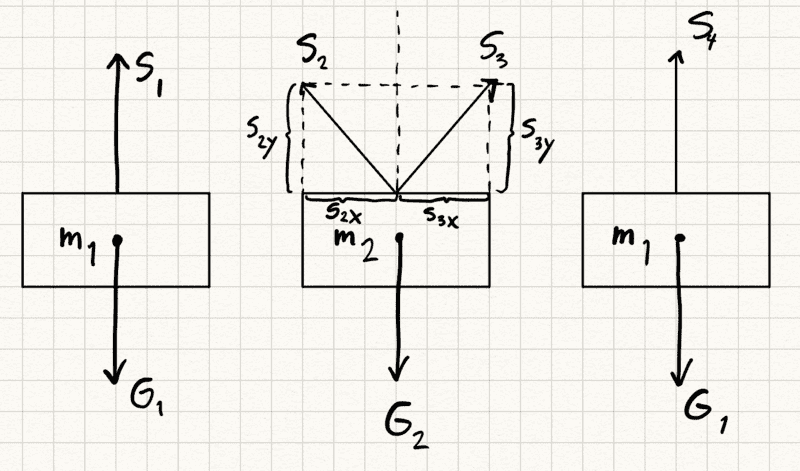
FBD:

Note: I believe I have solved a) correctly and am more confused about b).
a) I started with drawing the FBD. Knowing that the net sum has to be zero for the system to be at rest I used the left mass to find the tension on the rope: S₁ = G₁ = 15kg*9,81m/s² = 147,15 N. Now that I know the tension I moved over to the middle mass. I know G₂ = 147,15 N and that |S₁|=|S₂|=|S₃|=|S₄|. As the system is symmetric on each side I didn't do anything with the x-component of S₂ and S₃ on the middle mass, as they cancel out.

I know that S_2y + S_3y = G₂ or rather 2 * S_2y = G₂ to simplify as the system is symmetric. Therefore S_2y = G₂/2 = 147,15N / 2 = 73,575 N.

It looks like the system can be at rest, I just have to find the angle on the ropes on the middle mass.
I know that sin(θ) = S_2y / S₂.

θ = arcsin(S_2y / S₂) = arcsin(73,575N / 147,15N) = 30 degrees.

So the system is at rest when the angle between the mass and each rope is 30 degrees.b) I used the radius of pulley r=0,20m, the rope length s=3,0m and the length between pulleys (centre to centre) l=0,80m. Again, the system is symmetric so I will look at the left side. I will also use the connection points between the rope and the masses as their position. A simple diagram:

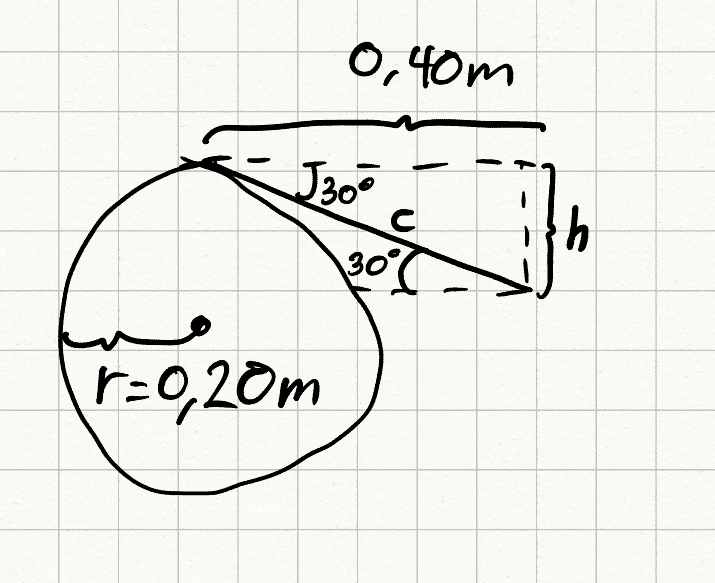
I can find the length h from a straight line between the pulley tops to the middle mass by doing the following:
tan(30deg) = h / 0,40m
h = 0,40m * tan(30deg) = 0,23. I can then find the rope length to the top of the pulley from the middle mass by:
sin(30deg) = h / c
c =h / sin(30deg) = 0,40m * tan(30deg) / sin(30deg) = 0,462m
Also, the rope length around the pulley is about a quarter circle: 0,40m*π / 4 = π / 10 = 0,314m.
The length from the leftmost point of the pulley and down to the left mass is 1,5m - 0,462m -0,314m = 0,724m ≈ 0,72m.

If we now make the coordinate system have its x-axis along the top of the pulleys, and the y-axis through the centre of the first pulley, the masses would have the following positions:
Left mass: (-0,20, -0,20-0,72) = (-0,20, -0,92)
Middle mass: (0,40, -0,23)
Right mass: (1,0, -0,92)

Is this correct? I feel like I'm missing a function to figure out how much rope goes around the pulley as I believe this will be more than a quarter circle if the middle mass weighs a lot more than the outer masses. But I'm not sure how to get started here.

As for c, I want to make sure I got b correct first, and I think it'll solve itself without being too difficult as the angle the system is at rest is only dependent on the masses and can also be found with arcsin(m₂ / 2m₁). Then I would just follow the process in b).

 

[erobz]

Note: Where the rope touches the pulley at point $P$ what is the relationship for the angle between that rope and a line joining $P$ to $O$ ($O$ is the center of the pulley)? Try to redraw your diagram to represent this better so it becomes clearer to you.

 

[kuruman]

I think you are making your life unnecessarily complicated. As @erobz remarked, your third drawing of the pulley detail is drawn incorrectly. For a pulley of finite size, the string will partially wrap around the pulley. Just imagine what the drawing would look like if the radius of each pulley were equal to the separation between the pulley centers!

I would use negligible zero radius for the two pulleys redraw the FBD and calculate the angle between the strings connected to the middle mass. Then I would use the given horizontal separation between masses and the angle to find the vertical position of the middle mass below the center-to-center separation of the pulleys.

Do yourself a favor and use symbols $m_1$ for the side masses, $m_2$ for the middle mass and $L$ for the separation between pulleys. In part (b) you can set $m_1=m_2$ and see what you get for the vertical position.

In part (c) you should check what happens to the angle when you change the ratio $m_2/m_1$ from zero to very large. If you have, say, 1 kg masses on the sides and the middle mass is that of a feather, the system will be at equilibrium and the angle between strings very close to 180°. However, if the middle mass is that of a battleship, the system cannot be at equilibrium. I would find at what ratio of masses equilibrium is untenable. Hint: somewhere between "feather" and "battleship".

 

[Steve4Physics]

Hi @Tlurk

You apparently haven’t given the original question in full, so we are guessing if your answers are appropriate.

As noted by @kuruman, your working could be a lot simpler if you used symbols. (Also, this minimises potential arithmetic and rounding errors.)

If this is not clear (and since your answer/working for part a) is correct) let me explain:

To check if the system can be at rest we need to show that there is some configuration where the net force on each mass is zero.

If such a configuration exists:
$T = m_1g$ (forces on an outer mass)
$2T \sin \theta = m_2g$ (vertical forces on the centre mass)

It is then trivial (with $m_1=m_2$) to show that $\theta = 30^o$ satisfies the equations. (In addition, it is useful to know that this answer is valid for any 3 equal masses and is independent of g.)

 

[Tlurk]

Thank you for answering!
So I redid a) using symbols, I'm not sure why I didn't do that in the first place so thanks for reminding me:

This matches my previous answer, but I can now change the masses without doing it over again.

For part b) I added a length of the rope R, made the Y-axis go through the centre of the left pulley, and the X-axis go through the centre of both pulleys. Now the length of the rope in total on the left half of the system is $$\frac{1}{2}R$$ and I can use the imaginary triangle drawn in the system overview in the figure above to find the length of the hypotenuse c:
$$\sin{\beta} = \frac{\frac{1}{2}L}{c}$$
$$c = \frac{L}{2\sin{\beta}}$$
The length of the rope from the left pulley (in other words the left pulley's Y-coordinate) is then given by:
$$\frac{1}{2}R - c$$ which can be written as $$\frac{1}{2}R - \frac{L}{2\sin{\beta}}$$ We find the angle beta or 1/2 alfa from a), so we don't have any unknowns variables here. R and L is of course chosen by us.

Now to find the height of m₂ I can use that $$\tan(\beta) = \frac{\frac{1}{2}L}{h}$$
$$h = \frac{L}{2\tan{\beta}}$$
And we know h will be the negative y-coordinate for m₂.

I think I got this down with a negligible radius at least, but I have to look some more into solving it with a larger radius for the pulleys, thanks a lot for the help so far!
As for erobz' answer, I realize the rope will be perpendicular to the line from P to O which gives me yet another right-angle triangle to work with. I have to think some more about this one.

 

[erobz]

Thank you for answering!
So I redid a) using symbols, I'm not sure why I didn't do that in the first place so thanks for reminding me:
View attachment 314767
This matches my previous answer, but I can now change the masses without doing it over again.

For part b) I added a length of the rope R, made the Y-axis go through the centre of the left pulley, and the X-axis go through the centre of both pulleys. Now the length of the rope in total on the left half of the system is $$\frac{1}{2}R$$ and I can use the imaginary triangle drawn in the system overview in the figure above to find the length of the hypotenuse c:
$$\sin{\beta} = \frac{\frac{1}{2}L}{c}$$
$$c = \frac{L}{2\sin{\beta}}$$
The length of the rope from the left pulley (in other words the left pulley's Y-coordinate) is then given by:
$$\frac{1}{2}R - c$$ which can be written as $$\frac{1}{2}R - \frac{L}{2\sin{\beta}}$$ We find the angle beta or 1/2 alfa from a), so we don't have any unknowns variables here. R and L is of course chosen by us.

Now to find the height of m₂ I can use that $$\tan(\beta) = \frac{\frac{1}{2}L}{h}$$
$$h = \frac{L}{2\tan{\beta}}$$
And we know h will be the negative y-coordinate for m₂.

I think I got this down with a negligible radius at least, but I have to look some more into solving it with a larger radius for the pulleys, thanks a lot for the help so far!
As for erobz' answer, I realize the rope will be perpendicular to the line from P to O which gives me yet another right-angle triangle to work with. I have to think some more about this one.

Why did your pulleys disappear in part (b)? The intermediate objective is to determine the angle of wrap around the pulley (you kind of need them represented in the analysis), then use it to find the length of the rope ( call it $l_2$) from the point of tangency on the pulley to $m_2$. The length $l_2$ will be a function of $L, r, \theta$ ( or $\beta$ - the angle $\theta$ I'm referring to is what you have as $90-\beta$ ). Then there will be more constraints that apply after you find that.

EDIT: I didn't catch that you were just testing the water with an approximation there. Good idea. Now it's on to the main event!

 

[kuruman]

Why did your pulleys disappear in part (b)? The intermediate objective is to determine the angle of wrap around the pulley (you kind of need them represented in the analysis), then use it to find the length of the rope ( call it $l_2$) from the point of tangency on the pulley to $m_2$. The length $l_2$ will be a function of $L, r, \theta$ ( or $\beta$ - the angle $\theta$ I'm referring to is what you have as $90-\beta$ ). Then there will be more constraints that apply after you find that.

EDIT: I didn't catch that you were just testing the water with an approximation there. Good idea. Now it's on to the main event!

Based on the statement of the problem, it seems to me that one needs not worry about the radii of the pulleys because they are not given or assumed known . That said, it is clear that the statement of the problem is @Tlurk's interpretation of what the problem gives and what it asks. No physics problem begins with "I have a system with two pulleys and $\dots~$"

To @Tlurk : Can you post the statement of the problem exactly as given to you?

 

[kuruman]

And we know h will be the negative y-coordinate for $m_2$.

How does knowing $h$ help you figure out the threshold value of $m_2$ above which there can be no equilibrium?

 

[erobz]

Based on the statement of the problem, it seems to me that one needs not worry about the radii of the pulleys because they are not given or assumed known . That said, it is clear that the statement of the problem is @Tlurk's interpretation of what the problem gives and what it asks. No physics problem begins with "I have a system with two pulleys and $\dots~$"

To @Tlurk : Can you post the statement of the problem exactly as given to you?

Yeah, I think the problem statement is missing some relevant information. If you notice they say in the analysis they use $r = 0.2 \, \rm{m}$ and $s= 3 \, \rm{m}$

b) I used the radius of pulley r=0,20m, the rope length s=3,0m and the length between pulleys (centre to centre) l=0,80m. Again, the system is symmetric so I will look at the left side. I will also use the connection points between the rope and the masses as their position. A simple diagram:

I assumed that it is just relevant information left out of the problem statement. ( in order to get numerical coordinates of the masses in (b) you need that information )

 

[Tlurk]

To @Tlurk : Can you post the statement of the problem exactly as given to you?

The problem is not in English, but translated it reads:
The figure shows two pulleys and three masses. You choose the value for the mass m, the starting position for the masses and the distance between the pulleys. Disregard the friction in the pulleys and the air resistance. Is it possible to make all the masses stay in place (system in equilibrium)? If so, what is the position of each mass? What happens if you change the weight of the middle mass? Draw a FBD for every mass and use Newton's laws to analyze the problem.


That is absolutely everything that's given.

Yeah, I think the problem statement is missing some relevant information. If you notice they say in the analysis they use $r = 0.2 \, \rm{m}$ and $s= 3 \, \rm{m}$

I assumed that it is just relevant information left out of the problem statement. ( in order to get numerical coordinates of the masses in (b) you need that information )

The values I used were just something I came up with to solve it numerically. But as I quickly discovered it was better to use symbols instead. I believe I have to take the pulley radius into consideration because the position of the outer masses is dependent on it, right? Anyways, now I've started working on finding the length around the pulley, so I will at least give it a try even if it's not needed.

 

[erobz]

So, it seems to me you can only answer (b) algebraically then (there are no values for anything except $\theta$ from part (a) - just parameters). The problem statement has left out the radius of the pulley or the length of the rope.

 

[Lnewqban]

Welcome, @Tlurk !

The question that makes absolutely no sense to me is :
" If so, what is the position of each mass?".

The spatial location of masses $m_1$ can be anywhere vertically.
The location of mass $m_2$ only depends on the distance between pulleys, as the value of the symmetrical angle of the rope is unique for each combination of $2m_1/m_2$.

 

[kuruman]

Thank you for posting the problem as given. The problem specifically says that you can choose the mass so choose $m$, the center-to-center separation so choose $L$ and the initial position of the masses. It seems to me that this means "choose the entire length of the rope". Any number greater than $L$ will do. But once you specify that, you will be expected to find the distance of each mass from the ceiling in terms of $L$, $m_1$ and $m_2$. I would start the rope horizontal with the side masses hanging symmetrically and then put the middle mass in place and look at the vertical displacements.

The problem says nothing about choosing the radius of a pulley which to me means assume that it is negligible. Then the horizontal coordinate of each mass will be fixed at ($-\frac{L}{2}$), ($0$) and ($+\frac{L}{2}$).

An interesting variation would be to make the three masses unequal.

 

[kuruman]

The spatial location of masses m1 can be anywhere vertically.

The full statement of the problem gives the choice of initial position. See post #13 about figuring out displacements in an "experiment" where you start with no mass in the middle and then hooking it on.

 

[Tlurk]

So, it seems to me you can only answer (b) algebraically then (there are no values for anything - just parameters). The problem statement has left out the radius of the pulley or the length of the rope.

I do believe that we're supposed to test a few different values to see how the system moves, eventually graphing the position, velocity and acceleration of each mass as that's what we've been doing to simpler systems so far. But as it's been quite a while since the last time I've had any physics subjects so I decided it would be easier to start in equilibrium (which I also feel the first question is leading us towards). Please do tell me if you think I should have a different approach.

I will try to solve it algebraically as you said. I think I need to if I want to import some of the functions I find underways to graph the movement as well. But I'm getting ahead of myself now and need to understand this on paper first.

The question that makes absolutely no sense to me is :
" If so, what is the position of each mass?".

The spatial location of masses $m_1$ can be anywhere vertically.
The location of mass $m_2$ only depends on the distance between pulleys, as the value of the symmetrical angle of the rope is unique for each combination of $2m_1/m_2$.

Yes, that's what I thought as well. The way the problem is given is why I've tried to introduce a rope length and pulley radius myself, to figure out the exact position of the masses.

 

[erobz]

The problem says nothing about choosing the radius of a pulley which to me means assume that it is negligible.

That's probably the case.

 

[kuruman]

$\dots~$ velocity and acceleration of each mass $\dots~$

What velocity and acceleration? Is this system not at equilibrium?

 

[erobz]

I do believe that we're supposed to test a few different values to see how the system moves, eventually graphing the position, velocity and acceleration of each mass as that's what we've been doing to simpler systems so far. But as it's been quite a while since the last time I've had any physics subjects so I decided it would be easier to start in equilibrium (which I also feel the first question is leading us towards). Please do tell me if you think I should have a different approach.

I will try to solve it algebraically as you said. I think I need to if I want to import some of the functions I find underways to graph the movement as well. But I'm getting ahead of myself now and need to understand this on paper first.

I expect you mean how the equilibrium position moves with different masses, as @kuruman is properly concerned about the interpretation here.

You can parameterize the radius too, It's just little extra trigonometric gymnastics.

 

[Tlurk]

What velocity and acceleration? Is this system not at equilibrium?

Well, yes, if the initial position of the middle mass makes the angle $$\beta = \arccos{\frac{m_2}{2m_1}}$$ but not if the initial position makes a different angle with the same masses. But as I said I'm getting to far ahead of myself now, and need to understand this fully at equilibrium first, as originally asked.

How does knowing $h$ help you figure out the threshold value of $m_2$ above which there can be no equilibrium?

I'm not really sure what you mean here. I guess $m_2 < 2m_1$ has to be true to make the $$arccos{\frac{m_2}{2m_1}}$$ valid which h depends on.

 

[erobz]

What velocity and acceleration? Is this system not at equilibrium?

Just a little scope creep!

 

[Lnewqban]

...
Yes, that's what I thought as well. The way the problem is given is why I've tried to introduce a rope length and pulley radius myself, to figure out the exact position of the masses.

Consider that in problems like this, including non-moving ideal pulleys (no mass, no friction, no translation), their function is limited to modify the direction in which the force is transferred by the rope or string.

You could simplify this particular problem to a summation of vectors representing all acting forces and their lines of action (respect to th ecentral body or mass), which reach a natural state of equilibrium.

Note that the vertical component of each of the two non-vertical actual force or rope tension must be of a magnitude equal to half the actual vertical force (weight of mass 2).

And, as suggested by @kuruman , the asymmetrical case:

[Edit: Incorrect diagram replaced with shown one]

 

[haruspex]

And, as suggested by @kuruman , the asymmetrical case:

View attachment 314786

I think you mean m3<m1 for β>α, m2<m1+m3.
I can’t see that β>60° is of special interest.

 

[Lnewqban]

I think you mean m3<m1 for β>α, m2<m1+m3.
I can’t see that β>60° is of special interest.

Thank you, @haruspex
The posted diagram was incorrect.
I am editing it.