System subject to a driving force

[LCSphysicist]

Homework Statement

All below

Relevant Equations

All below

The displacement of the end of a spring varies as

, the block on the spring is subject to a viscous force proportional to the velocity. Spring stiffness k.

(a)Find the displacement of the block:
(b)When γ -> 0

First of all, i have a doubt i we could start saying the component of the force is the imaginary component, seems plausible?

Anyway:

$x'' + yx' + wo²*x = wo²*d*sin(wt)$
$sin(wt) = cos(wt + 3pi/2)$ , x is Real part of z
$z'' + yz' + wo²z = wo²*d*e^{(wt + 3pi/2)i}$
$Solving for z = A*e^{i(wt + 3pi/2))$

(a)X=

+

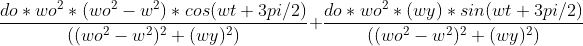(b)X =

+

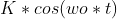
That's ok?

 

[jbriggs444]

You mention a parameter $y$. But you have not defined it. Presumably you mean for it to denote the viscosity. Naturally, this viscosity will be positive.

You mention a parameter $o$ which is always used as $o^2$. Plausibly you mean for this to denote the spring constant k.

You use a parameter $d$. But the parameter that is defined is $d_0$.

You use a parameter $\omega$. But the parameter that is defined is $\omega_d$.

Can you rewrite your first equation after having defined the variables it uses?

 

[jbriggs444]

Yes, i rushed, my bad.

Being a body subject to a driven force F, in a medium whose constant of viscosity (T^-1) is y, and being x the displacement of the body/system.

That does not match the problem statement in the original post. There the driver was at a specified position rather than delivering a specified force.

Can we have an accurate problem statement, please?

 

[LCSphysicist]

That does not match the problem statement in the original post. There the driver was at a specified position rather than delivering a specified force.

Can we have an accurate problem statement, please?

i tried to do the post in the cellphone, but made a huge confusion, it translate the message to my language, sorry. i deleted it. Anyway, now i think is better:

The block is attached to a cord that runs
over a pulley and is attached to a spring, as shown
The displacement of the end of the spring, subject to a driving force, varies as
$d*sin(w*t)$
$t>=0$
and the block, which is attached to the spring, is subject to a viscous force proportional to the velocity, Fs.

$Fs = -m*y*v$
Where v is the velocity of the body
and y is the damping coefficient [T^´-1]
m is the body mass.
and k is the spring stiffness
"

(a)Find the displacement of the block:
(b)When γ -> 0​

 

[haruspex]

In your first equation, I don't understand the $\omega_0^2x$ term. Shouldn’t there be a k in there somewhere?

 

[LCSphysicist]

In your first equation, I don't understand the $\omega_0^2x$ term. Shouldn’t there be a k in there somewhere?

Yes, there is k, but i assumed that k = m*wo², where wo is the natural frequency. I though it would be more interesting an answer in function of wo.

 

[haruspex]

Yes, there is k, but i assumed that k = m*wo², where wo is the natural frequency. I though it would be more interesting an answer in function of wo.

Ok, but it would have helped if you had defined $\omega_0$, which you wrote as $\omega o$. @jbriggs444 thought o was some other variable, and I assumed $\omega_0$ was a renaming of $\omega_d$.
Is y supposed to be $\gamma$?

I haven't checked the last parts of your solution, but I am a bit puzzled as to what happens when $\gamma<2\omega_0$.

 

[etotheipi]

Perhaps someone can explain to me the setup in #4. As far as I can tell, if we define the coordinate $y$ of the block as the distance below the horizontal level of the spring, then our equation of motion is$$mg - T - c\dot{y} = m\ddot{y}$$Now if we define another coordinate $x$ which is the horizontal distance of the end of the spring from the peg, that$$x = d + d_0\sin{\omega_d t}$$where $d$ is the average $x$ coordinate of the end of the spring. Then the total length of the spring at any given time is (assuming the whole wire is the spring, it shouldn't matter),$$L(t) = y + d + d_0\sin{\omega t}$$The force $T$ must then be $$T = k\delta(t) = k(L(t) - L_0) = k(y + d + d_0\sin{\omega t} - L_0)$$and finally our equation of motion is$$mg - k(d-L_0) - kd_0\sin{\omega t} = m\ddot{y} + c\dot{y} + ky$$Have I got that right, or did I miss something?

 

[jbriggs444]

If we were going to include gravity, we might consider buoyancy as well. But I see no need to include either. They are both equivalent to a fixed external force. Since we already have a spring in the problem, a fixed external force is equivalent to a change in the starting position.

We are not told the relaxed length of the spring. So we may as well do ourselves a favor and assume that the problem starts with the body at rest in its equilibrium position before the driver starts driving the spring.

 

[etotheipi]

If we were going to include gravity, we might consider buoyancy as well. But I see no need to include either. They are both equivalent to a fixed external force. Since we already have a spring in the problem, a fixed external force is equivalent to a change in the starting position.

We are not told the relaxed length of the spring. So we may as well do ourselves a favor and assume that the problem starts with the body at rest in its equilibrium position before the driver starts driving the spring.

Thanks, yes I forgot about buoyancy . So I will recast the equation in terms of a constant force plus that due to the tension$$f - T = m\ddot{y} + c\dot{y}$$How to deal with the term $T$ in a simple manner still does not seem obvious to me. In my original setup$$T = k(y + d + d_0\sin{\omega t} - l_0)$$maybe you would like to express$$\dot{T} = k\dot{y} + d\omega \cos{\omega t}$$and insert$$-k\dot{y} - d\omega \cos{\omega t} = m\dddot{y} + c\ddot{y}$$ $$m\dddot{y} + c\ddot{y} + k\dot{y} = - d \omega \cos{\omega t}$$which is now a third order equation which should still yield to a standard constant coefficients method of solution...

 

[LCSphysicist]

Ok, but it would have helped if you had defined $\omega_0$, which you wrote as $\omega o$. @jbriggs444 thought o was some other variable, and I assumed $\omega_0$ was a renaming of $\omega_d$.
Is y supposed to be $\gamma$?

I haven't checked the last parts of your solution, but I am a bit puzzled as to what happens when $\gamma<2\omega_0$.

Well, if this happens, we are going to complex solutions and i think we would need to get the real parts, so the therms with euler would convert to something like
$y = K*e^(-yt/2)*cos(w1t + α))$

w1² = $\omega_0^2 + y^2/4$)
About the problems of confusing the terms, i am still learning latex, actually i wrote all the equations in latex, but i probably made an error and so i prefer to write this in any program. Sorry

Actually i think all we hoping that this occurs
"I haven't checked the last parts of your solution, but I am a bit puzzled as to what happens when $\gamma<2\omega_0$."
Otherwise, the motion wouldn't be oscillation, right?

 

[etotheipi]

@LCSphysicist I think you are on track for the differential equation you wrote down in the OP, but AFAIK that doesn't describe the scenario given in the question?

 

[LCSphysicist]

@LCSphysicist I think you are on track for the differential equation you wrote down in the OP, but AFAIK that doesn't describe the scenario given in the question?

Sorry... what is AFAIK?

 

[etotheipi]

Sorry... what is AFAIK?

Oh, it's just "as far as I know" . I got that$$m\dddot{y} + c\ddot{y} + k\dot{y} = - d_0 \omega_d \cos{\omega_d t}$$