karush
Gold Member
MHB
- 3,240
- 5
$\tiny{t6.1.1}$
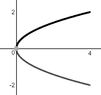
$\text{The solid lies between planes perpendiaular to the}$
$\text{$x$-axis at $x=0$ and $x = 4$.}$
$\text{The cross-scctions perpendicular to the axis on the interval
$0 \le x \le 4$}$
$\text{are squrares whose diagonals run for the parabola $\displaystyle f_a(x)=-\sqrt{x}$
to $\displaystyle f_b(x)=\sqrt{x}$}$
$\text{Find the volume of the solid}$$\textit{the area of the square whose diagonal is from $-\sqrt{x}$ to $-\sqrt{x}$ is}$
\begin{align*}\displaystyle
A_{square}(x)&=[\sqrt{2x}]^2 \\
&=2x
\end{align*}
ok just want to see if the area of the square is ok before
\begin{align*}\displaystyle
I&=\int_{0}^{4} ? \,dx
\end{align*}
View attachment 7421
$\text{The solid lies between planes perpendiaular to the}$
$\text{$x$-axis at $x=0$ and $x = 4$.}$
$\text{The cross-scctions perpendicular to the axis on the interval
$0 \le x \le 4$}$
$\text{are squrares whose diagonals run for the parabola $\displaystyle f_a(x)=-\sqrt{x}$
to $\displaystyle f_b(x)=\sqrt{x}$}$
$\text{Find the volume of the solid}$$\textit{the area of the square whose diagonal is from $-\sqrt{x}$ to $-\sqrt{x}$ is}$
\begin{align*}\displaystyle
A_{square}(x)&=[\sqrt{2x}]^2 \\
&=2x
\end{align*}
ok just want to see if the area of the square is ok before
\begin{align*}\displaystyle
I&=\int_{0}^{4} ? \,dx
\end{align*}
View attachment 7421