- #1
srekai
- 8
- 0
I did the problem, just want to validate my solution/approach
1. Homework Statement
Your car happens to have a fuzzy die hanging from the rear view mirror. As you round a curve that is approximately a circle of radius R you notice that the fuzzy die makes an angle θ with the vertical. What is the angle θ as a function of R and your speed v?
$$\sum F = ma$$
$$F = \frac{mv^2}{r}$$
There are 3 forces on the dice as shown in the free body diagram attachment
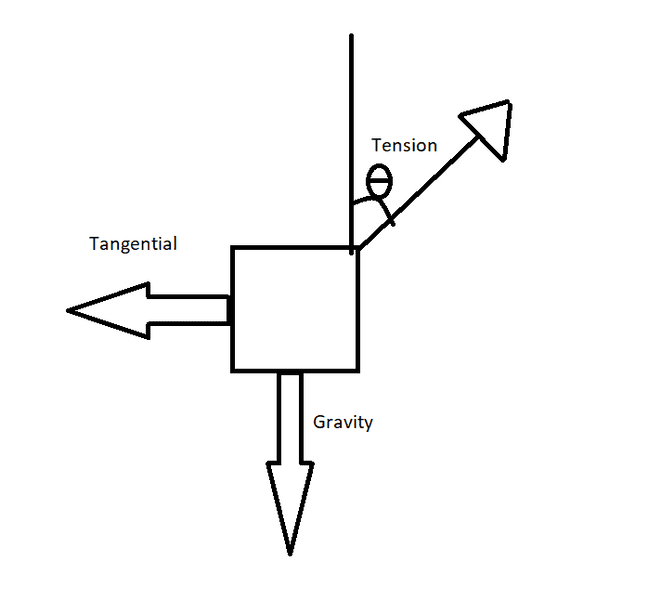
From this the sum of the vertical forces and horizontal forces must cancel out, so we can say
$$F_{\text{tension,y}} = F_{\text{gravity}}$$
$$F_{\text{tension}} \cdot cos \theta = F_{\text{gravity}}$$
$$F_{\text{tension}} \cdot cos \theta =mg$$
$$F_{\text{tension}}= \frac{mg}{cos \theta}$$
and
$$F_{\text{tension,x}} = F_{\text{tangential}}$$
$$F_{\text{tension}} \cdot sin \theta = F_{\text{tangential}}$$
$$F_{\text{tension}} \cdot sin \theta = \frac{mv^2}{r}$$
$$ \frac{mv^2}{r} = mg \cdot \frac{sin \theta}{cos \theta}$$
$$tan \theta = \frac{v^2}{rg}$$
$$\theta = tan^{-1}\frac{v^2}{rg}$$
1. Homework Statement
Your car happens to have a fuzzy die hanging from the rear view mirror. As you round a curve that is approximately a circle of radius R you notice that the fuzzy die makes an angle θ with the vertical. What is the angle θ as a function of R and your speed v?
Homework Equations
$$\sum F = ma$$
$$F = \frac{mv^2}{r}$$
The Attempt at a Solution
There are 3 forces on the dice as shown in the free body diagram attachment
From this the sum of the vertical forces and horizontal forces must cancel out, so we can say
$$F_{\text{tension,y}} = F_{\text{gravity}}$$
$$F_{\text{tension}} \cdot cos \theta = F_{\text{gravity}}$$
$$F_{\text{tension}} \cdot cos \theta =mg$$
$$F_{\text{tension}}= \frac{mg}{cos \theta}$$
and
$$F_{\text{tension,x}} = F_{\text{tangential}}$$
$$F_{\text{tension}} \cdot sin \theta = F_{\text{tangential}}$$
$$F_{\text{tension}} \cdot sin \theta = \frac{mv^2}{r}$$
$$ \frac{mv^2}{r} = mg \cdot \frac{sin \theta}{cos \theta}$$
$$tan \theta = \frac{v^2}{rg}$$
$$\theta = tan^{-1}\frac{v^2}{rg}$$
Attachments
Last edited:
