Task1: Vector Triangle: Calculate Resulting Speed

[supersander]

I'm having my semester test tomorrow, and I got this task from my teacher to do before the semester test.
:
By decomposition of forces apply these formulas for a right triangle:

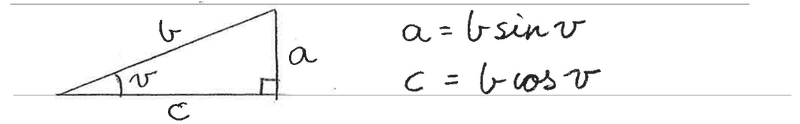
Task1:

An iceberg floats with the stream and wind. The power comes straight from the north with speed 3m / s. Draw this vector where the resulting speed of the iceberg to come forward as a vector. 1 cm shall be equal to 1 m / s. Calculate how large the resulting speed is using geometry or trigeometri.Would be very happy if anyone could help me with this, thank you very much!my attempt:

to the calculate resulting speed:

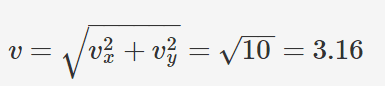
How is this? and how do i draw this as a vector?

 

[mfb]

There is some information missing, and the problem statement has a weird grammar.
Please post the full, exact problem statement, or try to find a better translation if the original is not English.

and how do i draw this as a vector?

In the same way the triangle is drawn.