- #1
- 668
- 68
Homework Statement
find the first four nonzero terms in the power series expansion of tan(x) about a=0
Homework Equations
[tex]\Sigma_{n=0}^{\infty} \frac{f^n (a)}{n!}(x-a)^n[/tex]
The Attempt at a Solution
Well the series has a zero term at each even n (0,2,4 etc)
for n=1 I got x, for n=3 I got [itex]\frac{x^3}{3}[/itex]
i ran into a problem while trying to compute n=5, since I got [itex]\frac{x^5}{10}[/itex] rather than [itex]\frac{2x^5}{15}[/itex] which is the answer. I assume that I must have differentiated wrong, so if someone could check the below derivatives I would appreciate it!
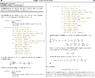
[tex]tan(x)[/tex](n=0)
[tex]sec^2(x)[/tex](n=1)
[tex]2tan(x)sec^2(x)[/tex](n=2)
[tex]2tan^2(x)sec^2(x)+2sec^4(x)[/tex](n=3)
[tex]4tan^3(x)sec^2(x)+4tan(x)sec^4(x)+8sec^4(x)tan(x)[/tex](n=4)
[tex]8tan^4(x)sec^2(x)+12tan^2(x)sec^4(x)+16tan^2(x)sec^4(x)+4sec^6(x)+32tan^2xsec^4(x)+8sec^6(x)[/tex](n=5)
As you can see in the n=5 expression plugging in x=0 reduces it to equaling 12; if it were instead equal to 16 I would have the correct expression.
Also, this method is very tedious so if anyone knows of an easier way please let me know!