- #1
johnrot
- 21
- 1
(I don't know what happened with my topic so I will post it again...)
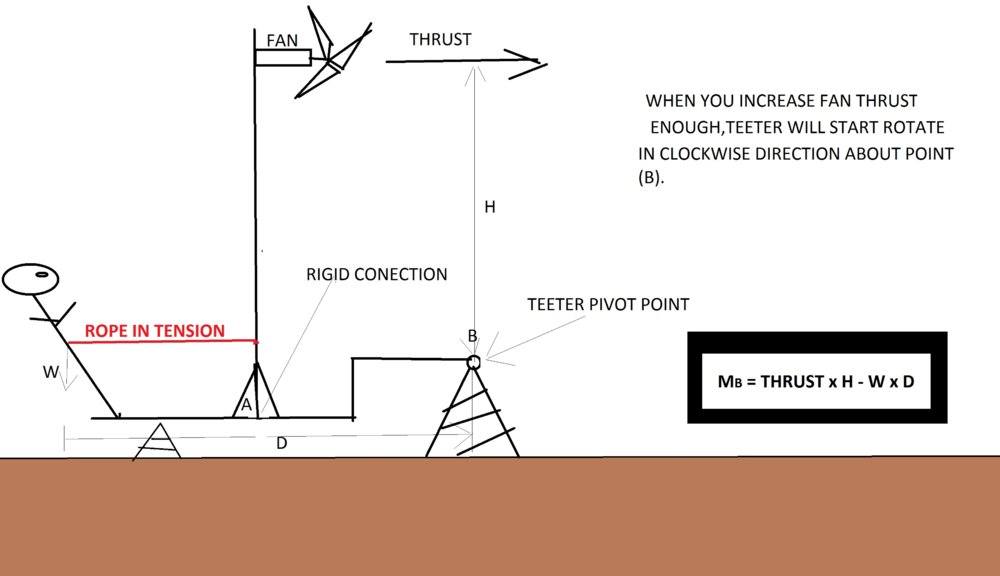
this is my half weird teeter with pivot point at (B)
and we have two solution for conection ,rigid conection and with universal joint..
this is example how type of conection can change direction of rotation..
basics question is :in what direction will teeter rotate about pivot point (B)..
rigid conection
universal joint conection
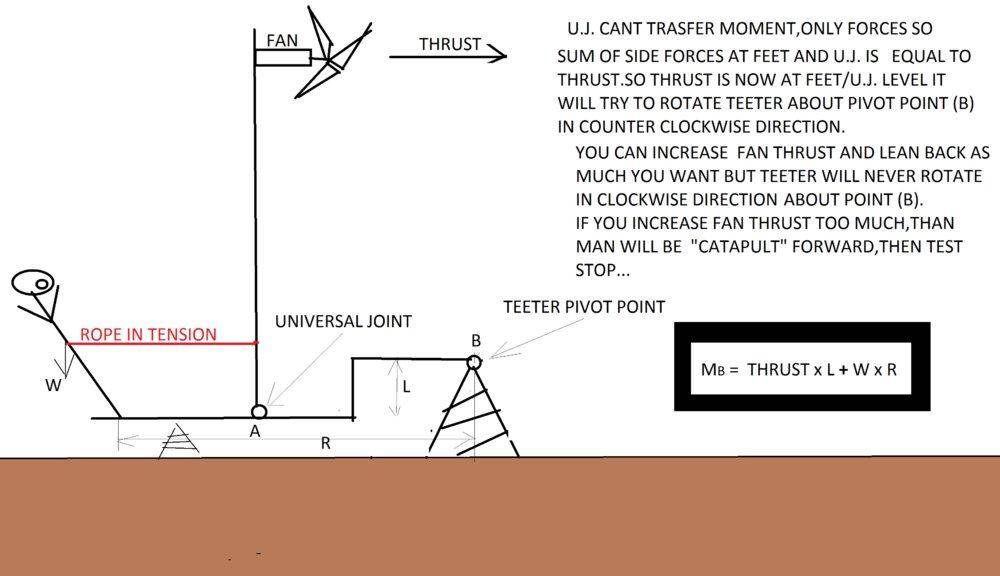 Do you agree with my conclusion and moment equation?
Do you agree with my conclusion and moment equation?
this is my half weird teeter with pivot point at (B)
and we have two solution for conection ,rigid conection and with universal joint..
this is example how type of conection can change direction of rotation..
basics question is :in what direction will teeter rotate about pivot point (B)..
rigid conection
universal joint conection
Last edited: