Tension force of block and rope

[Wes Turner]

Homework Statement

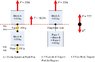
Block B hangs from Block A by a Rope 1. Rope 2 hangs below Block B.
Each block has a mass of 1.0 kg.
Each rope has a mass of 250 g.

The entire assembly is accelerating upward at 3.00 m/s^2 by force F.
A. What is F?
B. What is the tension at the top of Rope 1?
C. What is the tension at the bottom of Rope 1?
D. What is the tension at the top of Rope 2?

Homework Equations

F = ma
T = Sum(forces acting on that point)
The tension force at any point in the system = sum of forces acting at that point.

The Attempt at a Solution

The total mass of the system is 2 x 1000 g + 2 x 250 g = 2500 g
The net acceleration on the entire system = 3.00 m/s^2. So the force at any point is that acceleration x the mass below that point.
A. F = ma = 2500 g x 3.00 m/s^2 = 7500 g-m/s^2 = 7.4 N
B. F = ma = (250 g + 1000 g + 250 g) x 3.00 m/s^2 = 4500 g-m/s^2 = 4.5 N
C. F = ma = (1000 g + 250 g) x 3.00 m/s^2 = 3750 g-m/s^2 = 3.75 N
D. F = ma = 250 g x 3.00 m/s^2 = 750 g-m/s^2 = 0.75 N
And the tension on the bottom of Rope 2 = 0 N.

Did I get that right?

 

[stockzahn]

Is this scenario assumed to take place on Earth or in outer space?

 

[Wes Turner]

Is this scenario assumed to take place on Earth or in outer space?

On earth, sorry. g = 9.8 m/s^2.
I also just noticed that I got the answers off by 1 letter. I just edited the original post to fix that (I hope). Sorry

 

[stockzahn]

On earth, sorry. g = 9.8 m/s^2.

You didn't take into account all the acting forces. Try to draw a FBD and then apply Newton's 2nd law including all forces: $ma=\sum F_i$.

 

[Wes Turner]

You didn't take into account all the acting forces. Try to draw a FBD and then apply Newton's 2nd law including all forces: $ma=\sum F_i$.

I tried to do that, but all of the previous examples in the book made use of massless ropes. I wasn't sure what to do when they asked about a point midway in the system that is has mass both above and below it.

Here's the FBD for the entire system (I think):

 

[stockzahn]

I tried to do that, but all of the previous examples in the book made use of massless ropes. I wasn't sure what to do when they asked about a point midway in the system that is has mass both above and below it.

Here's the FBD for the entire system (I think):
View attachment 216566

Looks good. Now the force $F_{net}$ has to accelerate the entire mass with $a=3\;m/s$, hence $F_{net}=ma=T-w=\sum F_i$. You have two unknowns ($T,w$) but only one equation. You need another correlation to solve the problem (and since we are on earth...).

 

[Wes Turner]

Looks good. Now the force $F_{net}$ has to accelerate the entire mass with $a=3\;m/s$, hence $F_{net}=ma=T-w=\sum F_i$. You have two unknowns ($T,w$) but only one equation. You need another correlation to solve the problem (and since we are on earth...).

But isn't w just the weight of the system = 2500 g x 9.8 m/s^2 = 24500 g-m/s^2 = 24.5 N.

 

[stockzahn]

But isn't w just the weight of the system = 2500 g x 9.8 m/s^2 = 24500 g-m/s^2 = 24.5 N.

It's the weight force. But yes, that's what's necessary to answer the question of point A. Substituting $w$ by $mg$ and inserting it in the balance of forces yields the force $T$. I suppose you will then see how to calculate the points B-D, where, in your first attempt, you made the same mistake as in point A. The masses you took into account to solve the questions are correct.

 

[Wes Turner]

It's the weight force. But yes, that's what's necessary to answer the question of point A. Substituting $w$ by $mg$ and inserting it in the balance of forces yields the force $T$. I suppose you will then see how to calculate the points B-D, where, in your first attempt, you made the same mistake as in point A. The masses you took into account to solve the questions are correct.

I started down that path, but I got stymied when my intuition told me that the forces on the bottom end of Rope 2 should be zero, which they wouldn't by if I have to take into account both the mass below (zero) and above (2500 g) that point.

Does that point at the bottom of Rope 2 feel any tension forces? Intuitively, it seems like it should not. It's a point and points are massless, no?

But then I couldn't reconcile that with what would happen if I considered the whole thing upside down in a place where the up force is g and the down force is whatever it would take to cause the whole thing to accelerate downward at 3.00 m/s^2. But still, it seems like that bottom (now top) point should not feel any tension force.

 

[stockzahn]

I started down that path, but I got stymied when my intuition told me that the forces on the bottom end of Rope 2 should be zero, which they wouldn't by if I have to take into account both the mass below (zero) and above (2500 g) that point.

Does that point at the bottom of Rope 2 feel any tension forces? Intuitively, it seems like it should not. It's a point and points are massless, no?

But then I couldn't reconcile that with what would happen if I considered the whole thing upside down in a place where the up force is g and the down force is whatever it would take to cause the whole thing to accelerate downward at 3.00 m/s^2. But still, it seems like that bottom (now top) point should not feel any tension force.

To calculate the force at a certain point of a rope, you mentally cut it and apply forces to fulfill the kinematic conditions. That's what you explained in your first post:

The tension force at any point in the system = sum of forces acting at that point.

You have to take into account all the masses below to obtain the force in this point of the rope. Now what mass you have to accelerate, if you mentally cut the rope at it's very end?

 

[stockzahn]

PS.: Any solution regarding the point A by now?

 

[Wes Turner]

PS.: Any solution regarding the point A by now?

Do you mean the point just below Block A?

I see now that I didn't label the diagram very well. Here's a better version:

Now, is the net force on point R1a equal to 1000 g x 3.00 m/s^2 + 1500 g x 9.8 m/s^2?

If not, I can't think straight any longer tonight. Off for some sleep.

 

[stockzahn]

Do you mean the point just below Block A?

Sorry, misunderstanding. By point A, I meant question A (total force).

Now, is the net force on point R1a equal to 1000 g x 3.00 m/s^2 + 1500 g x 9.8 m/s^2?

No, just try to solve question A with

1) $ma=T-w$
2) $w=mg$

and I suppose the solution of the questions B-D becomes obvious.

If not, I can't think straight any longer tonight. Off for some sleep.

Good night from CET.

 

[Wes Turner]

It's the weight force. But yes, that's what's necessary to answer the question of point A. Substituting $w$ by $mg$ and inserting it in the balance of forces yields the force $T$. I suppose you will then see how to calculate the points B-D, where, in your first attempt, you made the same mistake as in point A. The masses you took into account to solve the questions are correct.

OK, maybe thinking a little more clearly now...

Here's another sketch for part (b), the tension on the top of Rope 1 (point R1a).

Fnet = T - w = ma = 2.5kg x a = T - 1.5kg x g
T - 1.5kg x 9.8m/s^2 = 2.5kg x 3m/s
T = 2.5kg x 3m/s + 1.5kg x 9.8m/s^2
T = 7.5N + 14.7N = 22.2N

I have to go to class now. I'll check back in later.

 

[stockzahn]

OK, maybe thinking a little more clearly now...

Here's another sketch for part (b), the tension on the top of Rope 1 (point R1a).
View attachment 216594 View attachment 216592

Fnet = T - w = ma = 2.5kg x a = T - 1.5kg x g
T - 1.5kg x 9.8m/s^2 = 2.5kg x 3m/s
T = 2.5kg x 3m/s + 1.5kg x 9.8m/s^2
T = 7.5N + 14.7N = 22.2N

I have to go to class now. I'll check back in later.

I'm sorry for the confusion regarding the expression "point". Try to mentally cut the system at the respective spot (as I drew for the four questions in the picture at the and of the post). The corresponding forces $F_a$ to $F_d$ act to accelerate all the masses below. Let's start with a) and solve the force balance for it.

$ma=F_a- \sum m_i g$

Now all the other questions b)-d) can be solved analogously. From the drawing you can see, what masses the forces $F_b$ to $F_d$ have to accelerate.

 

[Wes Turner]

Let me start over. I'm going to get this right if it kills me.

Let's start by calculating F. In my original post, I had it as 7.4N:

F = ma = 2500 g x 3.00 m/s^2 = 7500 g-m/s^2 = 7.4 N

But this ignores gravity. To get the correct values, I think I first need to calculate F_g, the force due to gravity on the entire system:
F_g = w = 2.5kg x g = 2.5kg x 9.8m/s² = 24.5N

To calculate F, I need a force that will achieve an acceleration of 3.0 m/s² plus overcome F_g.
F = ma = 2.5kg x (3.00m/s² + 9.8m/s²) = 2.5kg x 12.8m/s² = 32kg-m/s² = 32N

Please tell me if I have it right so far...

Thanks, WT

 

[stockzahn]

Let me start over. I'm going to get this right if it kills me.

Let's start by calculating F. In my original post, I had it as 7.4N:

But this ignores gravity. To get the correct values, I think I first need to calculate F_g, the force due to gravity on the entire system:
F_g = w = 2.5kg x g = 2.5kg x 9.8m/s² = 24.5N

To calculate F, I need a force that will achieve an acceleration of 3.0 m/s² plus overcome F_g.
F = ma = 2.5kg x (3.00m/s² + 9.8m/s²) = 2.5kg x 12.8m/s² = 32kg-m/s² = 32N

Please tell me if I have it right so far...

Thanks, WT

That's it! Now for all the other questions it's the same way to calculate the forces by taking into account the correct masses to be accelerated by the forces $F_b$ to $F_d$.

 

[Wes Turner]

That's it! Now for all the other questions it's the same way to calculate the forces by taking into account the correct masses to be accelerated by the forces $F_b$ to $F_d$.

Good. Here's an updated problem diagram and FBD for the entire system:

Do you see any errors here?

I noticed that you posted a thumbnail. Is it better if I post thumbnails instead of the full image?

 

[stockzahn]

Good. Here's an updated problem diagram and FBD for the entire system:
View attachment 216670 View attachment 216669
Do you see any errors here?

Well, according to your right picture the force balance yields $ma=F-F_g=32-24.5=7.5\;N$. The mass $m=2.5\;kg$, therefore $a=7.5\;N / 2.5\;kg = 3\;m/s^2$. That's the requested value for the acceleration and the answer of the question a) is obtained ($F_a=32\;N$). So I don't see an error.

I noticed that you posted a thumbnail. Is it better if I post thumbnails instead of the full image?

No, I don't see an advantage. It's just a habit in my case.

 

[Wes Turner]

Well, according to your right picture the force balance yields $ma=F-F_g=32-24.5=7.5\;N$. The mass $m=2.5\;kg$, therefore $a=7.5\;N / 2.5\;kg = 3\;m/s^2$. That's the requested value for the acceleration and the answer of the question a) is obtained ($F_a=32\;N$). So I don't see an error.

Ok, good. Here's my solution for Part (b):

In b.1 I divide the system at point R1a. The force on the entire system, F, is still 23N. The tension force on R1a is 19.2N, because it does not include the mass of Block A.

T = ma = 1.5kg x 12.8m/s² = 19.2N

I believe this is correct, but the diagram bothers me, because it does not show F_g, at least not explicitly. I suppose it is included in F, which would otherwise have a = 3.0m/s².

So how do I then draw the FBD. I thought we were to show all forces.

?

Using this approach, the answer (c) is T = 16N and (d) is T = 3.2N. The tension at R2b = 0N.

Comments?

Off to bed. Goodnight from PT.

 

[stockzahn]

In b.1 I divide the system at point R1a. The force on the entire system, F, is still 23N. The tension force on R1a is 19.2N, because it does not include the mass of Block A.
T = ma = 1.5kg x 12.8m/s² = 19.2N

Be cautious, when setting up the force balance. With the tension force $T_b$ (I called it $F_b$) it reads $ma=T_b-mg$.

So how do I then draw the FBD. I thought we were to show all forces.
?
Using this approach, the answer (c) is T = 16N and (d) is T = 3.2N. The tension at R2b = 0N.

Imagine the system in rest (no change of the state of movement (so $a=0$, static case). Now at the very end of the second rope, the tension force is zero, since below that point there is no mass to hold. Assuming homogeneous bodies and mentally going upwards from the bottommost point (as illustrated in the picture below the post): The tension in the system must increase linearly and at the connections between boxes and ropes there must be a discrete change of the slope (blue arrows). At the top the force holding the entire system must be equal to the weight force. If you want to find the tension force at a certain position, you can find it using the tension force progress (example: red arrows to find the tension force of 4.6 N somewhere in the lower box). The 4.6 N correspond to the weight force of the masses below.

Now, the entire system is accelerated. Like the tension force only has to hold the weight of the masses below in the static case, it only has to accelerate the masses below in the dynamic. If the entire force $F$ would be applied to the partial system, the acceleration would be higher than at the top and the top part would be overtaken by the lower parts of the system. The difference $F-T$ is used to accelerate the masses above.

Goodnight from PT.

Goodnight from CET.

 

[Wes Turner]

Imagine the system in rest (no change of the state of movement (so $a=0$, static case). Now at the very end of the second rope, the tension force is zero, since below that point there is no mass to hold. Assuming homogeneous bodies and mentally going upwards from the bottommost point (as illustrated in the picture below the post): The tension in the system must increase linearly and at the connections between boxes and ropes there must be a discrete change of the slope (blue arrows). At the top the force holding the entire system must be equal to the weight force. If you want to find the tension force at a certain position, you can find it using the tension force progress (example: red arrows to find the tension force of 4.6 N somewhere in the lower box). The 4.6 N correspond to the weight force of the masses below.

Your diagram is very helpful. I think I understand all of it except for the tension of 4.6N at what looks like the midpoint of Block B. I have annotated your drawing to add scales for mass and tension.

Did I do the T calculations correctly? If so, then it seems that your 4.6N should be 7.35N. No?

Edit: I keep making typos. I just corrected the last line in this post to say 7.35N, not 2.45N.
In the previous post, I transposed the digits in F and labeled it 23N, when I meant 32N. (sigh)

 

[Wes Turner]

If I understand it correctly, here are the tension forces for all of the points in the diagram, plus the ones at the top and bottom:

And here's a diagram showing the forces.

Please let me know if there are any errors.

Now, to get to the dynamic case, all I have to do is add the 3.00 m/s² acceleration force. Here's that table.

I don't have a diagram for that yet.

Please let me know if any errors.

Thanks

 

[stockzahn]

Did I do the T calculations correctly? If so, then it seems that your 4.6N should be 7.35N. No?

Sorry, that was my bad. You are of course right, the force should be around 7.4 N. Thanks for noticing.

 

[stockzahn]

Now, to get to the dynamic case, all I have to do is add the 3.00 m/s² acceleration force. Here's that table.

That's it, problem solved. Well Done!

 

[Wes Turner]

That's it, problem solved. Well Done!

Thanks very much for your help. Simplifying it to the static case was the breakthrough. Without that extra force, I was able to visualize it and then it was easy to add that force back in. Without your help, I may well have given up.