- #1
jamiebean
- 55
- 3
- Homework Statement
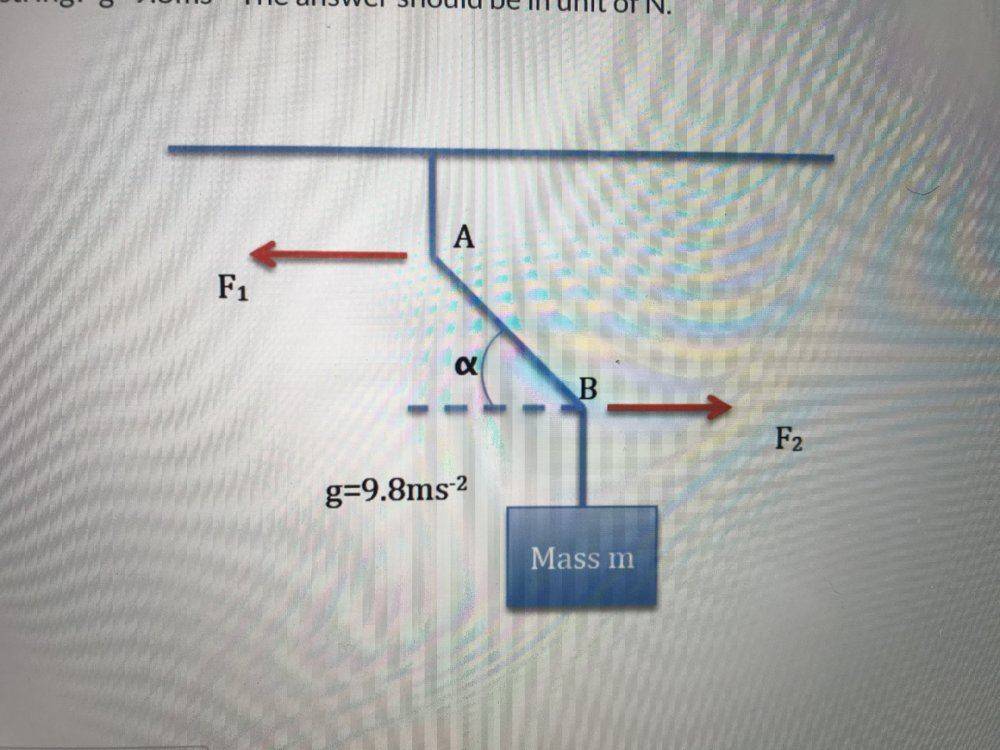
- A block of mass is suspended from the ceiling by a string as shown in the figure below. Two forces F1 and F2 cause the string to bend as shown in the figure. The section AB of the string makes an angle of α=43.5 degree with the horizontal line. The mass of the block is m=46.9kg. What is the tension of section AB of the string? g=9.8ms-2 The answer should be in unit of N.
- Relevant Equations
- f=ma
I am new to physics
I have no idea how the forces work and how to calculate the tension with f=ma
thank you very much..
I have no idea how the forces work and how to calculate the tension with f=ma
thank you very much..