- #1
adlewis90
- 2
- 0
I have tried to complete the following question by taking moments about point A, but to no avail. Could anybody help me with where i am going wrong. Do I need to include perpendicular distance?
The I-beam A-B shown below is supported by a cable at B and a pin at A. The cable is inclined at an angle, θ = 21° to the longitudinal axis of the beam. The beam supports a load, m, of 12 kN at a distance mx = 1.5 m from B.
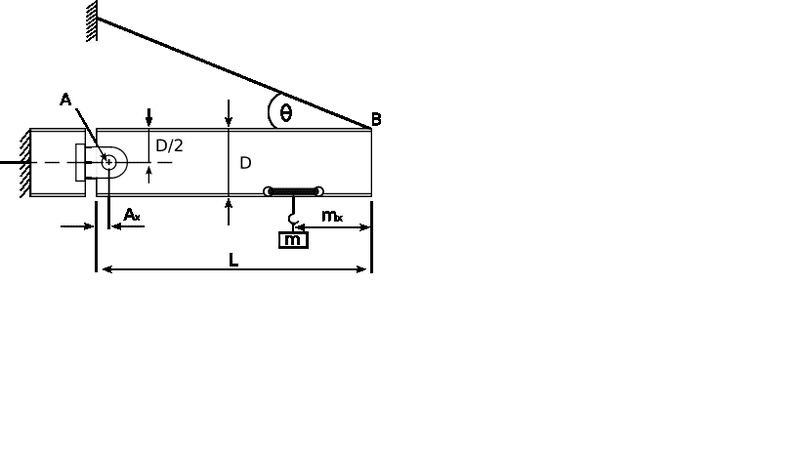
If the mass of the beam is 95 kg/m and its total weight can be assumed to act through the centre of gravity of the beam, calculate:
a) the cable tension, T
b) the resultant force acting on the pin at A.
Given:
Ax = 0.12 m, Beam Depth, D = 0.5 m, Beam Length, L = 5 m, Gravity, g = 9.81 m/s2
Part a)
Weight of beam = 4.65975 kN
By taking moments about A, T = 26.09±0.2 kN
Part b)
To determine the resultant at A, calculate the horizontal and vertical reactions AH and AV respectively:
AH = 24.36±0.2 kN
AV = 7.31±0.2 kN
Therefore, the resultant (using Pythagoras), R = 25.43±0.2 kN
Incorrect
Here is my solution to the cable tension
(4.88)(T)(sin21)+(111.834x0.06)-(4.5479x10^3)(2.44)-(12x10^3)(3.38)=0
1.7488(T)=+6.7098+11.0968x10^3+40.56x10^3
1.7488(T)=51650.0902
(T)= (51.65x10^3)/1.7488 =29.53kn
The I-beam A-B shown below is supported by a cable at B and a pin at A. The cable is inclined at an angle, θ = 21° to the longitudinal axis of the beam. The beam supports a load, m, of 12 kN at a distance mx = 1.5 m from B.
If the mass of the beam is 95 kg/m and its total weight can be assumed to act through the centre of gravity of the beam, calculate:
a) the cable tension, T
b) the resultant force acting on the pin at A.
Given:
Ax = 0.12 m, Beam Depth, D = 0.5 m, Beam Length, L = 5 m, Gravity, g = 9.81 m/s2
Part a)
Weight of beam = 4.65975 kN
By taking moments about A, T = 26.09±0.2 kN
Part b)
To determine the resultant at A, calculate the horizontal and vertical reactions AH and AV respectively:
AH = 24.36±0.2 kN
AV = 7.31±0.2 kN
Therefore, the resultant (using Pythagoras), R = 25.43±0.2 kN
Incorrect
Here is my solution to the cable tension
(4.88)(T)(sin21)+(111.834x0.06)-(4.5479x10^3)(2.44)-(12x10^3)(3.38)=0
1.7488(T)=+6.7098+11.0968x10^3+40.56x10^3
1.7488(T)=51650.0902
(T)= (51.65x10^3)/1.7488 =29.53kn