Tension in string pulling two carts

In summary, the pulley system does not have the same tension on each side because of the mass in between.
  • #1
annamal
387
33
Homework Statement
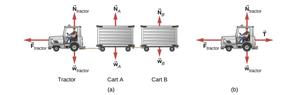
Figure attached shows a baggage tractor pulling luggage carts from an airplane. The tractor has mass 650.0 kg, while cart A has mass 250.0 kg and cart B has mass 150.0 kg. The driving force (820t) acting for a brief period of time accelerates the system from rest and acts for 3.00 s. Acceleration is 0.7805t. a) What is the horizontal force acting on the connecting cable between cart A and B at this instant? Assume friction is negligible.
Relevant Equations
F - T = m*a
820t - T = m*0.7805t
T = 820t - m*0.7805t
What would I use as mass? Mass of cart A, or mass of cart A and tractor?
F - T = m*a
820t - T = m*0.7805t
T = 820t - m*0.7805t
I am confused what I would use as mass? Mass of cart A, or mass of cart A and tractor?
 

Attachments

  • Screen Shot 2022-03-23 at 6.57.50 PM.png
    Screen Shot 2022-03-23 at 6.57.50 PM.png
    16 KB · Views: 174
Physics news on Phys.org
  • #2
As with any such question involving interacting masses that can move somewhat independently, draw a separate FBD for each mass. Each FBD should only show forces and accelerations directly related to the mass in question.
 
  • #3
haruspex said:
As with any such question involving interacting masses that can move somewhat independently, draw a separate FBD for each mass. Each FBD should only show forces and accelerations directly related to the mass in question.
cart A's formula: -T + T -Ff = m*a?
 
  • #4
Why have you assumed the two tensions are the same?
 
  • #5
Mister T said:
Why have you assumed the two tensions are the same?
In a pulley system, the tensions are the same, why aren't they the same for this tractor pulling carts?
 
  • #6
annamal said:
In a pulley system, the tensions are the same, why aren't they the same for this tractor pulling carts?
Because of the mass in between. We can only assume tensions are the same both sides of a pulley when there is no friction at the axle and either:
- it is a constant velocity arrangement (maybe static), or
- the pulley has negligible mass

The same applies for linear motion of a body between two strings. In the present case, there is no friction, but the body has mass and is accelerating.

Also, what is Ff in your equation? There is no mention of friction.
 
Last edited:
  • #7
haruspex said:
Because of the mass in between. We can only assume tensions are the same both sides of a pulley when there is no friction at the axle and either:
- it is a static arrangement, or
- the pulley has negligible mass

Also, what is Ff in your equation? There is no mention of friction.
I think it is negligible
 
  • #8
annamal said:
I think it is negligible
"a) What is the horizontal force acting on the connecting cable between cart A and B at this instant? Assume friction is negligible."

What instant is the problem referring to?
Should we assume it is at the end of the 3 seconds period?

Because the cables linking the three rolling masses do not stretch, the given acceleration is the same for each of those masses.
Cart B can't "see" what forces are beyond the A-B cable; therefore, you can simplify the solution by drawing a free body diagram for B that stops at that cable midpoint.
 
  • #9
annamal said:
In a pulley system, the tensions are the same, why aren't they the same for this tractor pulling carts?
If the pulley has mass, the tensions are not the same. Likewise, for the cart attached to the tractor. Once you master this line of reasoning, it's valuable to think about what happens when the cables are not massless.
 
  • Like
Likes Lnewqban
  • #10
Mister T said:
If the pulley has mass, and is accelerating, the tensions are not the same.
 
  • #11
Ok, well I solved it until
T = 820t - m*0.7805t. I am just confused which mass I put for m. Mass of cart A or mass of cart A and tractor.
 
  • #12
annamal said:
Ok, well I solved it until
T = 820t - m*0.7805t. I am just confused which mass I put for m. Mass of cart A or mass of cart A and tractor.
That's because you are not using free body diagrams. The diagram will show the forces acting on the object. The vector sum of those forces equals the mass of that object times the acceleration.
 
  • #13
Mister T said:
That's because you are not using free body diagrams. The diagram will show the forces acting on the object. The vector sum of those forces equals the mass of that object times the acceleration.
Free body digram for A:
T2 (tension from string tractor to cart A) <--- A ---> T (tension on string from A to B)
T2 = 820t - m (mass of tractor)*0.7805t
T2 - T = m*a --> T = T2 - m*a = 820t - mT (mass of tractor)*0.7805t = mA (mass of cartA)*0.7805t
Is this correct? I am assuming the tractor and carts are accelerating at the same rate?
 
  • #14
annamal said:
Free body digram for A:
T2 (tension from string tractor to cart A) <--- A ---> T (tension on string from A to B)
T2 - T = m*a
Since this follows from a free body diagram of A, then ##m## is the mass of A.
 
  • Like
Likes Lnewqban

FAQ: Tension in string pulling two carts

What is tension in a string?

Tension in a string is the force that is transmitted through the string when it is pulled tight. It is the result of the string being stretched and is always directed along the length of the string.

How does tension affect the movement of two carts?

When two carts are connected by a string, the tension in the string will cause both carts to move. The direction of movement will depend on the direction in which the string is pulled and the relative masses of the two carts.

What factors affect the tension in a string?

The tension in a string is affected by the force applied to it, the length of the string, and the properties of the string itself, such as its elasticity and material. The angle at which the string is pulled can also affect the tension.

How can tension be calculated in a string?

To calculate the tension in a string, you will need to know the force applied to the string, the length of the string, and the angle at which it is being pulled. You can then use the formula T = F * cos(θ) / L, where T is the tension, F is the applied force, θ is the angle, and L is the length of the string.

How can tension in a string be increased or decreased?

The tension in a string can be increased by applying a greater force to the string or by decreasing its length. It can be decreased by applying a smaller force or by increasing the length of the string. Changing the angle at which the string is pulled can also affect the tension.

Similar threads

Is there any friction in this case?
Replies
12
Views
844
Tension from two carts & hanging object on pulley
Replies
7
Views
3K
What is the work done on cart by the string?
Replies
1
Views
1K
Two carts are forced apart by a compressed spring
Replies
21
Views
3K
Explanation for Newton II giving negative mass in my Physics lab results please
2
Replies
44
Views
2K
Tension in a string which connects 3 pulleys
Replies
12
Views
582
Coefficient of Friction question for a cart going down a wooden ramp
Replies
18
Views
2K
Impulse and Momentum: Ball and cart connected by a cord
Replies
24
Views
3K
Acceleration of a cart immediately after the system is released
Replies
15
Views
3K
Push/Pull Force of wheeled cart on an incline
Replies
7
Views
3K

Hot Threads

Recent Insights

Back
Top